Card Shuffling Problem
by Zoran Horvat
Problem Statement
There are N cards in the deck. Write the program which shuffles the deck so that all cards are evenly distributed over multiple shuffles.
Example: Deck consists of four cards (1, 2, 3 and 4). One possible shuffling is: 3, 1, 2, 4.
Keywords: Cards, shuffling, probability, Fisher-Yates algorithm.
Problem Analysis
When speaking of shuffling a sequence of numbers, we can come to a difficulty to explain what does the shuffling mean in terms of distinguishing "well shuffled" from "poorly shuffled" sequence. Take two numbers: 1 and 2. Is the sequence [1, 2] shuffled? Or is the sequence [2, 1] shuffled better? Don't be tempted to believe that the latter one is, so to say, better than the previous. Better stance for comparing sequences would be to ask the following question: How often does the shuffling process produce sequence [1, 2] compared to sequence [2, 1]? Basically, it is not the sequence that is considered shuffled or not, it is the algorithm which produces proper or improper shuffling. So we are now stepping aside and looking at the sequence of sequences produced by the shuffling algorithm. It should be obvious that both sequences are legal when shuffling two numbers. It only remains to see whether shuffling algorithm produces these sequences in a sufficiently random manner.
For example, we could test whether both sequences appear equally often when algorithm is run many times. Observe this sequence of sequences: [[1, 2], [2, 1], [1, 2], [2, 1], [1, 2], [2, 1]]. Each of the sequences appears three times in six runs of the algorithm. Looks perfect, does it? But on the second look, it appears that sequence [1, 2] always precedes sequence [2, 1]. Let's take a look at Markov chains of sequences, i.e. to analyze how often transitions are made between the two sequences produced on the output. The result goes like this: Out of 5 transitions, we have [[1, 2], [2, 1]] occurring 3 times and [[2, 1], [1, 2]] occurring 2 times. There is no trace of transitions [[1, 2], [1, 2]] and [[2, 1], [2, 1]]. Like this algorithm is utterly unable to repeat any of the sequences twice in a row, although truly random algorithm would have to produce the same sequence on the output once on every two attempts on average. So this algorithm doesn't seem to be a proper shuffling algorithm after all.
But now again, we could write an algorithm that produces this sequence of sequences: [[1, 2], [1, 2], [2, 1], [2, 1], [1, 2], [1, 2], [2, 1], ... ]. That algorithm would become perfect on both accounts: Appearances of particular sequences and appearances of particular transitions. But still it's obviously flawed as we always know the next sequence when previous two sequences are known. And there goes the idea: If we take Markov chains of length 2, we would quickly find that sequences [[1, 2], [2, 1], [1, 2]] and [[2, 1], [1, 2], [2, 1]] never appear on the output (sic!). So yes, the algorithm is flawed and it can be demonstrated formally.
Now we have seen three criteria for analyzing the shuffling produced by an arbitrary algorithm. We can devise an enhanced algorithm that performs perfectly on all three criteria, but then still find out yet another test on which it fails, namely to find one particular property of perfect shuffling (whatever should it be) that the algorithm does not satisfy. So what should we do? The answer is quite simple: Proper shuffling algorithm should not bother about conditions and criteria that sequences should meet, but it should better think of how to satisfy distribution of numbers within each particular sequence. Should this distribution be "honest", or in formal terms: unbiased, then we would rest assured that all sequences produced by such an algorithm would natively be well shuffled. In literature, you will find definitions of proper shuffling that range from trivial to very general, so general that they cannot be fully applied in practice.
For example, consider this criterion: A sequence is random if it has every property that is shared by all infinite sequences of independent samples of random variables from the uniform distribution.
Well, this sounds as if it has embodied all the possibilities. Should the theoretically perfect sequence have any property that it satisfies, then well formed algorithmically-produced sequence should definitely pass the test of that particular property. But alas, this definition is so broad that it cannot possibly be applied in practice in its full extent. (On a related note, this statement was given by Joel N. Franklin in a paper published in Mathematics of Computation journal back in 1963.) To bridge the gap between theory and practice, different authors have devised quite an impressive suite of tests that can be applied to sequences in order to measure their "properness".
It is beyond the scope of this article to discuss these tests. Further on we will focus on devising an unbiased algorithm and hope for the best when its output comes to the testing phase.
Solution
In the previous section we have identified pitfalls that threaten the shuffling algorithms. Simple conclusion on how to avoid the pitfalls is to code a simple unbiased algorithm. Whichever bias is introduced in order to avoid problems regarding some sequence test, that bias will become the root cause to falling another sequence test. So it's best to avoid them as a whole.
Shuffling algorithm that does not introduce any bias is the one that attempts to place numbers to positions in the array in such way that for any given position all the numbers are equally (and independently!) likely to be placed on that position.
So let's start with the first position. We have N numbers awaiting to be shuffled, we need to pick one to place it on position 1. If we pick any of them at random and place it on position 1, then position 1 is filled in an unbiased manner. This leaves us with N-1 numbers remaining and N-1 positions to be filled. If first position was filled properly with this algorithm, then why not to apply the same thinking to the second position? Let's pick up another random number out of N-1 and place it on the second position. Now we should stop at this point to think again - is there any dependency induced between the two numbers that were picked up? Does the first number somehow affect the selection of the second one, because if it does then our algorithm is bound to fail. To see whether shuffling of the first two positions is really random, we should calculate probabilities that any numbers out of N are placed on the first two positions. We start from the stance that random numbers generator used to pick one out of N and then one out of N-1 numbers is unbiased - this is actually a fundamental requirement.
Probability that any number out of N is picked for the first position is 1/N. Probability that any other number is picked up for the second position is then determined by a sequence of two events: first, that this number was not picked up in the first draw out of N and second, that the number was picked in the second draw out of N-1. We could write these two probabilities as following:
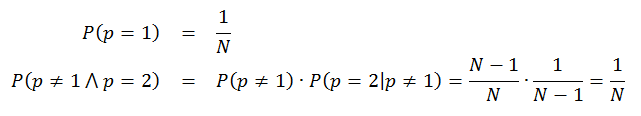
These expressions show probability that any given number occupies position p after shuffling has taken place. Note that we could multiply the probabilities for p=2 because these probabilities are independent - it shows how important is the prerequisite that random number generator produces independent numbers. Now we can extend the analysis to any particular position k between 1 and N: a number is not picked in any of the steps before k, and then it is picked up in step k when only N-k+1 numbers remain to be shuffled:
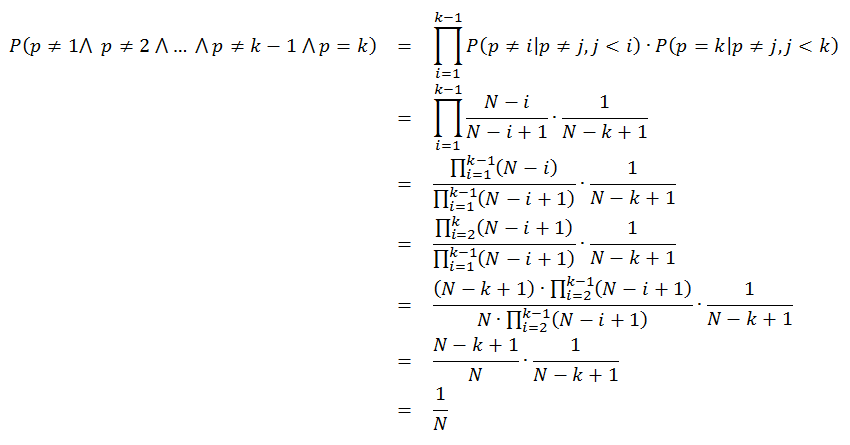
From this analysis we can conclude that the proposed algorithm indeed shuffles numbers in an independent way - any number is equally likely to be placed on any position in the output sequence and its placing there does not depend on placing of any other number in the sequence.
Now that we have all the elements, we can write down the algorithm. Only one small modification will be made, dictated by the technology - we will first solve the number at position N, then at N-1, and so on until position 1 is resolved. The reason is quite simple - we're dealing with random number generators that generate numbers between 0 and K for any given K, which then saves one arithmetic operation that would be required to shift the range into N-K thru N. Here is the algorithm:
a[1..n] - array of numbers that should be shuffled
for i = n downto 2
begin
k = random number between 1 and i
Exchange a[i] and a[k]
end
That is all. Note that there is no need to shuffle the number at position 1 in this implementation because that is the only number remaining - it is already shuffled by definition, so to say. For further reference, this algorithm is known as Fisher-Yates shuffle. There are some other algorithms available, some of them meeting other needs (e.g. to generate two arrays - non-shuffled and shuffled), but this one presented above is quite sufficient in most of the practical settings. It shuffles an array of numbers in time proportional to length of the array and also shuffles it in-place so that no additional space is needed.
Implementation
Implementation of the Fisher-Yates shuffling algorithm is straight-forward and we will step into it without further deliberation.
using System;
namespace Cards
{
class Program
{
static void Shuffle(int[] cards)
{
for (int i = cards.Length - 1; i > 0; i--)
{
int index = _rnd.Next(i + 1); // Generates random number between 0 and i, inclusive
int tmp = cards[i];
cards[i] = cards[index];
cards[index] = tmp;
}
}
static void Main(string[] args)
{
while (true)
{
Console.Write("Enter number of cards (0 to quit): ");
int n = int.Parse(Console.ReadLine());
if (n <= 0)
break;
int[] cards = new int[n];
for (int i = 0; i < n; i++)
cards[i] = i + 1;
Shuffle(cards);
for (int i = 0; i < n; i++)
Console.Write("{0,4}", cards[i]);
Console.WriteLine();
}
}
static Random _rnd = new Random();
}
}
Demonstration
Below is the output produced by the shuffling code.
Enter number of cards (0 to quit): 10
2 1 9 4 8 5 7 10 3 6
Enter number of cards (0 to quit): 5
5 4 1 3 2
Enter number of cards (0 to quit): 3
3 1 2
Enter number of cards (0 to quit): 14
10 7 8 4 1 13 14 12 9 6 11 3 5 2
Enter number of cards (0 to quit): 20
10 2 20 11 3 16 5 17 14 19 1 15 9 8 12 13 6 18 7 4
Enter number of cards (0 to quit): 0
On the first glance arrays indeed seem to be shuffled. But to be more certain we would have to apply several randomness tests, which is full heartedly suggested as a stand-alone exercise.
Follow-Up Exercises
Now that we have completed an initial run of the algorithm and obtained a few shuffled sequences out of it, the reader is suggested to turn attention to analyzing the results produced.
- Write the code that statistically calculates probabilities that any particular number occurs on any particular position in the shuffled array. Tell whether results are satisfying. For more keen users - measure confidence intervals for the distribution in order to formally evaluate the distribution.
- For a relatively small array lengths (e.g. up to 5), construct Markov chains of length 1 and analyze whether all transitions between successive sequences produced by the algorithm are equally likely. Once again, apply confidence interval analysis to the result.
- Pick up the literature and find appropriate tests that could be applied to evaluate the shuffling algorithm. Write code that applies them to results produced by the algorithm.
If you wish to learn more, please watch my latest video courses

Beginning Object-oriented Programming with C#
In this course, you will learn the basic principles of object-oriented programming, and then learn how to apply those principles to construct an operational and correct code using the C# programming language and .NET.
As the course progresses, you will learn such programming concepts as objects, method resolution, polymorphism, object composition, class inheritance, object substitution, etc., but also the basic principles of object-oriented design and even project management, such as abstraction, dependency injection, open-closed principle, tell don't ask principle, the principles of agile software development and many more.
More...

Design Patterns in C# Made Simple
In this course, you will learn how design patterns can be applied to make code better: flexible, short, readable.
You will learn how to decide when and which pattern to apply by formally analyzing the need to flex around specific axis.
More...

Refactoring to Design Patterns
This course begins with examination of a realistic application, which is poorly factored and doesn't incorporate design patterns. It is nearly impossible to maintain and develop this application further, due to its poor structure and design.
As demonstration after demonstration will unfold, we will refactor this entire application, fitting many design patterns into place almost without effort. By the end of the course, you will know how code refactoring and design patterns can operate together, and help each other create great design.
More...

Mastering Iterative Object-oriented Development in C#
In four and a half hours of this course, you will learn how to control design of classes, design of complex algorithms, and how to recognize and implement data structures.
After completing this course, you will know how to develop a large and complex domain model, which you will be able to maintain and extend further. And, not to forget, the model you develop in this way will be correct and free of bugs.
More...
About

Zoran Horvat is the Principal Consultant at Coding Helmet, speaker and author of 100+ articles, and independent trainer on .NET technology stack. He can often be found speaking at conferences and user groups, promoting object-oriented and functional development style and clean coding practices and techniques that improve longevity of complex business applications.
Elsewhere
Video Courses
- Making Your C# Code More Object-oriented
- Beginning Object-oriented Programming with C#
- Collections and Generics in C#
- Design Patterns in C# Made Simple
- Refactoring to Design Patterns
- Mastering Iterative Object-oriented Programming in C#
- Making Your C# Code More Functional
- Making Your Java Code More Object-oriented
- Writing Purely Functional Code in C#
- Tactical Design Patterns in .NET: Creating Objects
- Tactical Design Patterns in .NET: Control Flow
- Tactical Design Patterns in .NET: Managing Responsibilities
- Advanced Defensive Programming Techniques
- Writing Highly Maintainable Unit Tests
- Improving Testability Through Design
Articles
- Here is Why Calling a Virtual Function from the Constructor is a Bad Idea
- What Makes List<T> So Efficient in .NET?
- Nondestructive Mutation and Records in C#
- Understanding Covariance and Contravariance of Generic Types in C#
- Using Record Types in C#
- Unit Testing Case Study: Calculating Median
- More...