Unit Testing Case Study: Calculating Median

by Zoran Horvat
November 02, 2021

In this article, we shall investigate one technique of designing unit tests which stems from the concept of Abstract data types.

Problem Statement

Here is the problem statement: Write appropriate unit tests which are demonstrating correctness of a function which calculates median of a collection. Namely, tests should verify correctness of an implementation of interface defined as:

public interface IMedianTarget<T> where T : IComparable<T>
{
    T GetMedian();
}

The GetMedian() method returns median of elements contained in the object implementing the interface. Median is defined as “the value separating the higher half from the lower half of a data sample” (quoted from Wikipedia ). It is safe to assume that the object contains at least one element, i.e., that the median exists.

In the rest of this article, we shall analyze the requirements and produce unit tests that are satisfying the requirements.

Analyzing Requirements

Unit tests should entail directly from requirements, rather than from any technical analysis, let alone from implementation. When building tests from requirements, it is beneficial to observe system under test (SUT) as an Abstract data type (ADT). We are only allowed to express statements regarding SUT which are coming from requirements.

To illustrate benefits from this approach, assume one possible implementation of the median. We can order items from the collection and then select the one that stands in the middle. Shall we construct a test case by specifying the collection and then the value we consider a correct answer? (E.g., for data 2, 5, 1, 3, 4, median value is 3). Consider possible test implementation based on this idea.

protected Func<IEnumerable<int>, IMedianTarget<int>> SutFactory { get; }

[Theory]
[InlineData(3, 2, 5, 1, 3, 4)]
public void SpecificData_GetMedianReturnsExpectedValue(
    int median, params int[] data) =>
    Assert.Equal(median, this.SutFactory(data).GetMedian());

This test, however correct, is an example of incorrect reasoning. It is based on our intimate understanding of SUT’s implementation, while it should be based on customer’s requirements. How do we see that this test is tied to implementation? That is obvious: We know precise answer to the question which value is median. How could we know it if we didn’t calculate it on our own while preparing the test data?

And here is the true problem with this process. What would happen if we, engineers, misjudged the requirements? What if value 3 in test data above is not the correct answer? Wouldn’t our passing test then assure us it is safe to ship software which is in effect flawed? – Yes, of course it would, and the reason for that is that the test was not designed from the side of requirements, but rather from the side of their technical implementation. In the rest of this article, we shall correct the issue and come up with a better set of tests.

Analyzing Requirements – One More Time

User’s requirements consist of technical constraints (those defining the type subdued to tests), and of a substantial definition of behavior, in form of the median definition. Prior is a given. We can safely assume that all technical prerequisites listed in requirements are met before tests are run. Latter is what requirements had to say about expected behavior of the system under test.

Let’s dissect the requirement then: Value separating the higher half from the lower half of a data sample.

For one thing, we understand that we are looking for a value which is contained in the sequence. There is the first unit test: Median calculation method must return a value from the collection.

Second, we encounter statement that median separates higher half of the collection, which immediately tells us the second unit test: Median calculation method must return a value which, together with all values greater or equal to itself, forms at least one half of the collection.

Lastly, the rest of the statement is that median separates lower half of the data. Following previous logic with the higher half, we devise the last unit test: Median calculation method must return a value which, together with all values less or equal to itself, forms at least one half of the collection.

These unit tests are entailed directly from requirements, and do not derive from implementation. Even more, implementation is considered abstract, as in the sense of an Abstract data type. We do not know the type that implements them, but we only know abstract attributes of that type, like those about separating higher half of data from the lower half.

Below is full implementation of the testing class, which defines three unit tests that we have discovered. Testing class is using XUnit library.

public abstract class MedianTests
{
    protected Func<IEnumerable<int>, IMedianTarget<int>> SutFactory { get; }

    private static int[][] TestNumbers { get; } =
    {
        new[] { 2, 5, 1, 3, 4 }
    };

    public static IEnumerable<object[]> Data =>
        TestNumbers.Select(args => new object[] { args });

    [Theory, MemberData(nameof(Data))]
    public void GetMedianReturnsExistingValue(int[] data) =>
        Assert.Contains(
            this.SutFactory(data).GetMedian(),
            data);

    [Theory, MemberData(nameof(Data))]
    public void GetMedianSeparatesHigherHalf(int[] data) =>
        Assert.True(
            data.Count(x => x >= this.SutFactory(data).GetMedian()) >=
            data.Count() / 2);

    [Theory, MemberData(nameof(Data))]
    public void GetMedianSeparatesLowerPart(int[] data) =>
        Assert.True(
            data.Count(x => x <= this.SutFactory(data).GetMedian()) >=
            data.Count() / 2);
}

Take a note of Data and TestNumbers properties. Their format is the result of xUnit’s quirk about specifying test data via a class member. But, once it is done right, we will be able to add more arrays of numbers into the TestNumbers definition, and each array will be passed to one test run of each test method.

Applying the Tests

So far, we have developed abstract tests – tests that apply to an interface. To apply them to a class implementing that interface, we need two items: The implementation class itself, and a concrete derived testing class specializing to that implementation.

Consider implementation class which wraps around a list.

public class ListMedian<T> : IMedianTarget<T> where T : IComparable<T>
{
    public ListMedian(IEnumerable<T> content)
    {
        this.Content = content.ToList();
    }

    private List<T> Content { get; }

    public T GetMedian()
    {
        this.Content.Sort();
        return this.Content[this.Content.Count / 2];
    }
}

This class is holding a private list containing all the data to which it is applied. When the time comes to get the median, this class will sort the list and then select element at its middle, just as requirements have defined it.

We plan to subdue this class to abstract tests developed above. Remember, tests class is abstract because it lacks SUT factory function. And SUT factory is missing because it doesn’t know a concrete type to instantiate. To complete the testing class, we need a derived tests class which specializes to ListMedian<T> implementation class.

public class ListMedianTests : MedianTests
{
    protected override Func<IEnumerable<int>, IMedianTarget<int>> SutFactory =>
        data => new ListMedian<int>(data);
}

This class satisfies all requirements of the test runner: It is a public class, exposing public void methods decorated with Fact or Theory xUnit attributes. These methods are coming from its base, abstract MedianTests class, but test runner will pay no attention to where test methods are coming from, so long as they exist.

Needless to say, all three unit tests will pass for the sorting implementation of IMedianTarget<T>.

Refactoring the Class

Once we have assured that our implementation class is satisfying tests, we can declare that all the requirements have been satisfied, and happily ship the product.

Alternatively, we may consider improvements to the implementation. For instance, in the ListMedian<T> class, we notice that underlying list is sorted every time the GetMedian() method is invoked:

public T GetMedian()
{
    this.Content.Sort();
    return this.Content[this.Content.Count / 2];
}

Now that we have unit tests to save us from regressions, we can make improvements to the class with little fear. Below is the ListMedian<T> implementation which wraps sorting operation into a Lazy<List<T>> object, so to ensure that actual sorting is only performed once during the lifetime of an object.

public class ListMedian<T> : IMedianTarget<T> where T : IComparable<T>
{
    public ListMedian(IEnumerable<T> content)
    {
        this.Content = content.ToList();
        this.Sorted = new Lazy<List<T>>(this.SortAndGet);
    }

    private List<T> SortAndGet()
    {
        this.Content.Sort();
        return this.Content;
    }

    private List<T> Content { get; }
    private Lazy<List<T>> Sorted { get; }

    public T GetMedian() =>
        this.Sorted.Value[this.Content.Count / 2];
}

If we run the tests now, we will see that they are still all passing. Even after inflating the class’s implementation a bit, we are sure that implementation is satisfying requirements and that we can safely ship it to production.

Selecting Test Data

The last mandatory step before we call the testing class done is to select representative testing data. We shall start from requirements once again, to discover which data will have the best chance of discovering discrepancies between requirements and implementation.

For instance, it makes sense to test implementation for the smallest data collection that satisfies the requirements: The one consisting of a single element.

public abstract class MedianTests
{
    ...
    private static int[][] TestNumbers { get; } =
    {
        new[] { 7 },            // new case
        new[] { 2, 5, 1, 3, 4 }
    };
    ...
}

With this test case, we have covered one edge case. More edge cases can be found by reading the median definition again: “the value separating the higher half from the lower half of a data sample”. Here, we find at least two axes around which different possible implementations will rotate. One axis is data size parity, where precise definition of “half” differs when collection has even number of elements, opposed to a collection with odd number of elements.

Here is the augmented set of test data:

public abstract class MedianTests
{
    ...
    private static int[][] TestNumbers { get; } =
    {
        new[] { 7 },
        new[] { 6, 1, 4, 2, 3, 5 },  // new case
        new[] { 2, 5, 1, 3, 4 }
    };
    ...
}

Another axis defines repeated values equal to the median. There, we find several test cases, where repeated value appears next to the median right before it, right after it, or on both sides.

public abstract class MedianTests
{
    ...
    private static int[][] TestNumbers { get; } =
    {
        new[] { 7 },                 // single element
        new[] { 6, 1, 4, 2, 3, 5 },  // even count
        new[] { 2, 5, 1, 3, 4 },     // odd count
        new[] { 3, 5, 1, 4, 3, 2 },  // repeated left
        new[] { 4, 2, 4, 3, 1, 5 },  // repeated right
        new[] { 2, 3, 3, 4, 1, 3 },  // repeated both
        new[] { 2, 1, 4, 2, 3 },     // repeated left
        new[] { 2, 1, 3, 4, 3 },     // repeated right
        new[] { 2, 3, 2, 2, 1 }      // repeated both
    };
    ...
}

We have discovered total of 9 collections that are representative, according to requirements. Each collection applies to each of the three unit tests, making total of 27 tests executed upon any implementation of the IMedianTarget<T> interface. Needless to say, custom implementation ListMedian<T> is passing all 27 test cases.

This exercise has shown that it is possible to construct both the tests and test data by only testing against the abstract data type built from the requirements. That is still not to say that the entire test harness can be constructed in this way. In the remainder of this article, we shall introduce another implementation of the target interface, which will outline cases where implementation will start affecting tests again.

Introducing Alternate Implementation

Existing implementation, the ListMedian<T> class, is sorting the data before selecting the median. While that solution is correct, it is slow on large collections. Customers have requested a faster implementation, so here it is. Below is an optimized implementation which is only partitioning portions of data that are known to contain the median. (For more information about this algorithm, please refer to exercise Finding Kth Smallest Element in an Unsorted Array .)

public class PartitioningMedian<T> : IMedianTarget<T> where T : IComparable<T>
{
    public PartitioningMedian(IEnumerable<T> data)
    {
        this.Data = data.ToArray();
        this.Median = new Lazy<T>(() => this.FindKthSmallest(this.Data.Length / 2));
    }

    private T[] Data { get; }
    private Lazy<T> Median { get; }

    public T GetMedian() =>
        this.Median.Value;

    private T FindKthSmallest(int k)
    {
        int offset = 0;
        int count = this.Data.Length;

        while (true)
        {
            T pivot = FindPivot(offset, count);
            (int smaller, int larger) = this.Partition(offset, count, pivot);

            if (k < offset + smaller)
            {
                count = smaller;
            }
            else if (k < offset + count - larger)
            {
                return pivot;
            }
            else
            {
                offset = offset + count - larger;
                count = larger;
            }
        }
    }

    private T FindPivot(int offset, int count) =>
        count < 3 ? this.Data[offset]
        : this.SmallerOrEqual(
            this.GreaterOrEqual(this.Data[offset], this.Data[offset + count - 1]),
            this.Data[offset + count / 2]);

    private T SmallerOrEqual(T a, T b) =>
        a.CompareTo(b) <= 0 ? a : b;

    private T GreaterOrEqual(T a, T b) =>
        a.CompareTo(b) >= 0 ? a : b;

    private void Swap(int i, int j) =>
        (this.Data[i], this.Data[j]) = (this.Data[j], this.Data[i]);

    private (int smaller, int larger) Partition(int offset, int count, T pivot)
    {
        int smallerPos = offset - 1;
        int equalPos = offset + count;
        int largerPos = offset + count;

        while (smallerPos < equalPos - 1)
        {
            int comparison = this.Data[smallerPos + 1].CompareTo(pivot);
            if (comparison < 0)
            {
                smallerPos += 1;
            }
            else if (comparison == 0)
            {
                equalPos -= 1;
                this.Swap(smallerPos + 1, equalPos);
            }
            else
            {
                equalPos -= 1;
                largerPos -= 1;
                if (equalPos < largerPos) this.Swap(largerPos, equalPos);
                if (smallerPos < equalPos - 1) this.Swap(smallerPos + 1, largerPos);
            }
        }

        return (smallerPos - offset + 1, offset + count - largerPos);
    }
}

This implementation is much longer than the former one, the ListMedian<T> class. But, as a consolation, another set of tests has shown that this class runs four to five times faster than the prior one when subdued to collections containing hundreds of thousands or millions of items. Diagram below was produced using BenchmarkDotNet library, and it demonstrates clear benefits of using the PartitioningMedian<T> class to calculate medians. But, is the class functionally correct?

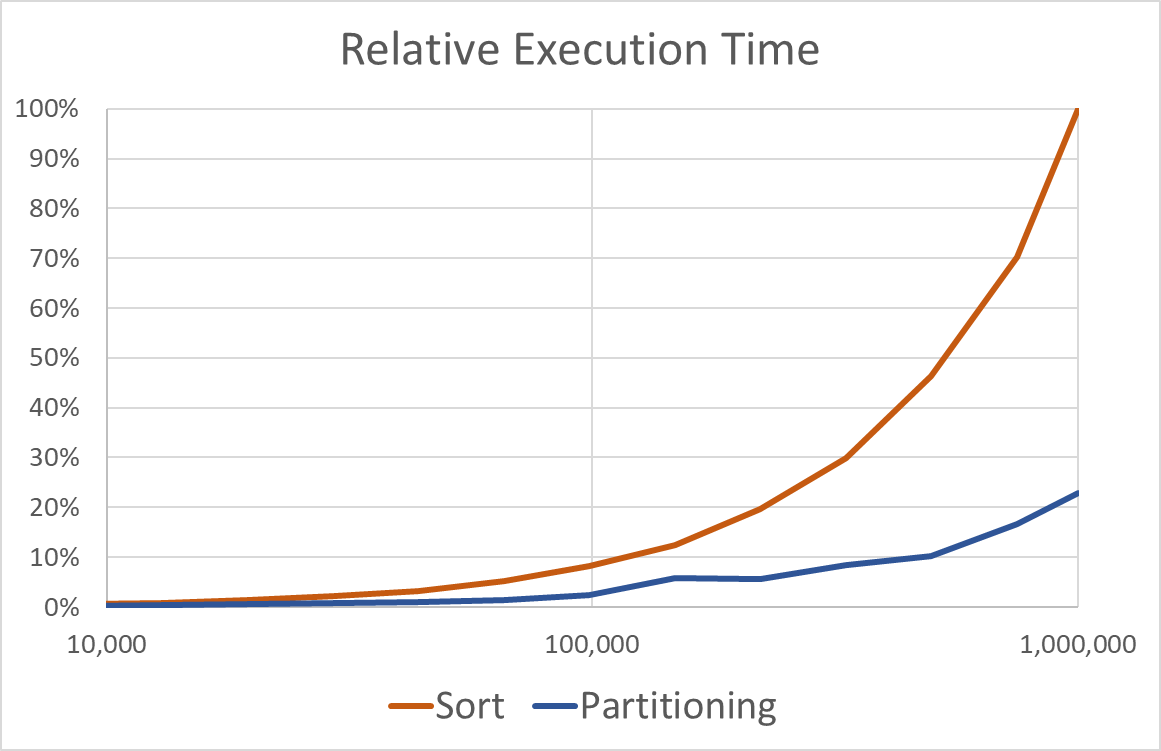
To test whether the class is operating as expected, we shall subdue it to the same set of tests as the prior class. For that purpose, we must implement another concrete testing class, this time specializing the SUT factory function to PartitionMedian<T>.

public class PartitioningMedianTests : MedianTests
{
    protected override Func<IEnumerable<int>, IMedianTarget<int>> SutFactory =>
        data => new PartitioningMedian<int>(data);
}

That is all we had to do to install another batch of 27 test cases, this time trying the new class in the solution. Immediate conclusion is that this class is satisfying the requirements at least to the same extent as the first class does.

However, there is one distinction between these two classes. If you read the FindPivot method in the PartitioningMedian<T> class, you will notice that it contains branching, depending on how many elements the collection has:

private T FindPivot(int offset, int count) =>
    count < 3 ? this.Data[offset]
    : this.SmallerOrEqual(
        this.GreaterOrEqual(this.Data[offset], this.Data[offset + count - 1]),
        this.Data[offset + count / 2]);

Collection that has one or two elements will never reach the negative branch. Consequently, we must ensure that these collections are also included in test data. You will discover these special cases easily if you keep track of code coverage metric.

In this particular case, all relevant test cases were included in the base testing class. But if it were not the case, we would still have an option to add more test cases in the derived PartitioningMedianTests class. Additional test cases would be designed to try features that are specific to this class. In other words, we have ended up designing white-box tests after all. But only after exhausting all the options we had at our disposal through tests of an ADT.

Summary

In this article, we have analyzed the problem of testing one practical algorithm, which calculates median of a data collection. You have learned that it can be beneficial to look at the implementation through lens of the Abstract data type (ADT). If you follow the idea through, you will end up designing abstract unit tests, which do not depend on implementation – nor do they repeat fallacies in logic that passed uncaught in the implementation itself.

By the end of this analysis, we have developed alternate implementation, which also satisfies the same test cases, enforcing our belief that implementation is truthfully satisfying the requirements.

The last discovery that was made while testing the alternate implementation is that ADT might not be sufficient to fully define implementation. Some decisions are specific to one implementation, and do not exist in others. That is where white-box testing comes back to the table, helping us design additional test cases specific to one implementation.

---