Moving Zero Values to the End of the Array

by Zoran Horvat
June 11, 2015

Problem Statement

Given an unsorted array of integer numbers, write a function which transforms the array so that all numbers that are equal to zero are moved towards the end of the array. Non-zero elements should be moved to the beginning of the array, while still preserving their relative order.

Example: Suppose that array [4, 1, 0, 2, 0, 0, 5, 3] is passed to the function. After the function executes, the array should contain values [4, 1, 2, 5, 3, 0, 0, 0].

Analysis

We could approach this problem from the mathematical induction point of view. The goal of the exercise is to produce an array which has the quality of having its zeros pushed towards its end. The mathematical induction now comes to the picture. If we could start with an initial array which possesses the quality we want, and if we could add one element at the time to the array, while in each step preserving the quality, then we could gradually build the final, complete array which also possesses the same quality.

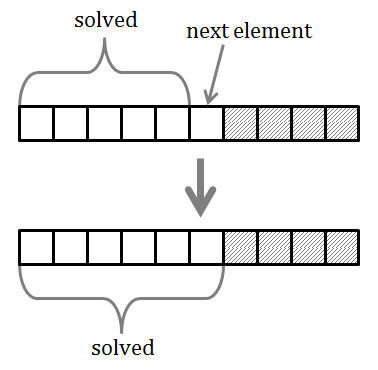
This idea sounds very simple and it is also simple to prove that it will work correctly. In mathematical induction we normally start with the initial state. In this example, we can say that an empty subarray satisfies the constraint from the problem statement. It contains no elements, so there is no element to violate the constraint.

Similarly, a subarray with only one element also possesses the desired quality. Being zero or non-zero, this single element cannot break the constraint.

So the problem boils down to solving the case with multiple elements in the subarray. We can set the inductive hypothesis that the subarray with k (k > 0) elements satisfies the constraint. Our goal is to extend the subarray with the element at position k+1 in such way that the quality is preserved.

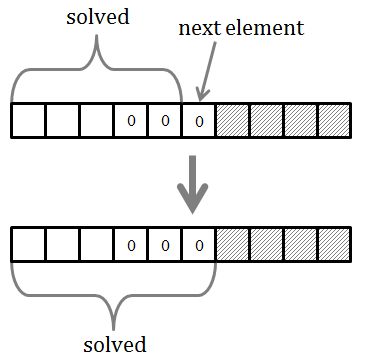
This operation will then depend on the value of the element at position k+1. If that element is zero, then it will not violate the constraint and the k+1 subarray will still possess the required quality. Picture below shows this case.

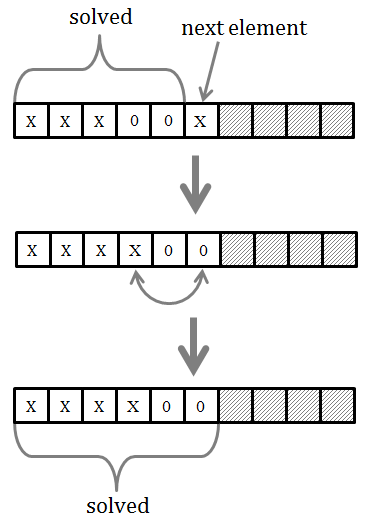
If the element at position k+1 is non-zero, then it will violate the constraint and cause the k+1 subarray to lose the quality of having all zeros near the end of the array. Our task is then to restore that quality. We can easily do that by swapping the non-zero element with the first zero element in the sequence of zeros, as shown in the picture below. In that way, the sequence of zeros will occupy the end of the array and the requested quality will be restored again.

This operation has one special case. It could happen that we encounter a non-zero element without visiting any zero element before it. In that case, the non-zero element is not violating the array quality and there is nothing to do with it. This case is shown in the following picture.

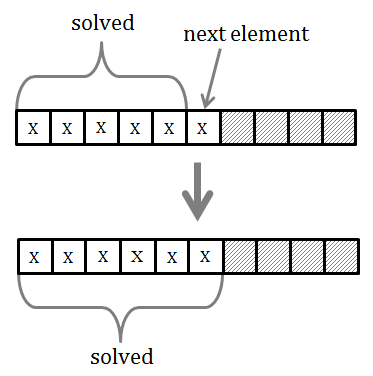
When all the elements of the array are exhausted, the complete array will be brought into state with all zero elements moved to its end. This completes the inductive proof of correctness of this algorithm.

Solution

Below is the pseudocode of the function which moves zeros to the end of the array.

function MoveZeros(a in/out, n)
    -- a – array of integers
    -- n – length of the array
Begin

    i = 0  -- index of the first zero
    while i < n and a[i] <> 0
        i = i + 1

    j = i  -- index of next number to process
    while j < n
        begin
            if a[j] <> 0 then
                begin
                    a[i] = a[j]
                    a[j] = 0
                    i = i + 1
                end
            j = j + 1
        end
end

This function will work properly on any array, and that is what we have proved using mathematical induction. But the problem with this function that it is a bit complicated. We can make it shorter by noticing that the first loop, which looks for the first occurrence of zero in the array, is not required. Without that loop, the non-zero element will just be swapped with itself, which is a null operation and has no effect. This case is presented in the figure below.

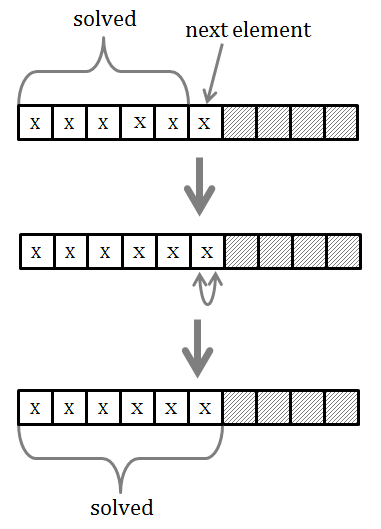
Bottom line is that we can eliminate the first loop entirely:

function MoveZeros(a in/out, n)
    -- a – array of integers
    -- n – number of elements
begin
    i = 1  -- next place to put non-zero element
    for j = 1 to n
        begin
            if a[j] <> 0 then
                begin
                    swap(a[i], a[j])
                    i = i + 1
                end
        end
end

function swap(x in/out, y in/out)
begin
    temp = x
    x = y
    y = temp
end

This implementation relies on a single loop in the function, but this time it must implement the proper swap function. Previous solution didn’t have to perform full swap of values because we knew that one of the values is zero.

Simplified Solution

Anyway, this implementation leads us to even better simplification. The whole process until this moment was driven by an inductive hypothesis that subarray up to the current position is solved. This means that all zeros that existed in that subarray are properly moved to its end. At this point, we are ready to relax the constraints.

Let’s say that we only want the final array to have this quality of having its zeros moved to the end. That is precisely what the problem statement says.

So, what can we do with the previous solution to make it simpler? The answer is that we don’t have to move zeros immediately. We can leave that step for the end, simply because we know that all values to move are equal to zero. Here is the solution:

function MoveZeros(a in/out, n)
    -- a – array of integers
    -- n – number of elements
begin

    i = 1 – index where to put next non-zero

    for j = 1 to n
        if a[j] <> 0 then
            begin
                a[i] = a[j]
                i = i + 1
            end

    while i <= n
        a[i] = 0

end

This solution is both simple and efficient. Every element of the array is copied at most once. It is based on the idea that inductive hypothesis can be relaxed, provided that it is re-established again before completing the operation.

Implementation

Below is the C# Console application with all three distinct implementations of the function that were discussed in this exercise.

using System;

namespace MoveZeros
{

    class Program
    {

        private static Random random = new Random();

        static int[] CreateArray(int n)
        {

            int[] array = new int[n];

            for (int i = 0; i < n; i++)
                array[i] = random.Next(6);

            return array;

        }

        static void Print(int[] a)
        {
            foreach (int value in a)
                Console.Write("{0,2}", value);
            Console.WriteLine();
        }

        static void MoveZerosFull(int[] a)
        {

            int i = 0;
            while (i < a.Length && a[i] != 0)
                i++;

            for (int j = i; j < a.Length; j++)
            {
                if (a[j] != 0)
                {
                    a[i++] = a[j];
                    a[j] = 0;
                }
            }

        }

        static void MoveZerosOneLoop(int[] a)
        {

            int i = 0;
            for (int j = 0; j < a.Length; j++)
                if (a[j] != 0)
                {
                    int tmp = a[i];
                    a[i] = a[j];
                    a[j] = tmp;
                    i++;
                }

        }

        static void MoveZeros(int[] a)
        {

            int i = 0;

            for (int j = 0; j < a.Length; j++)
                if (a[j] != 0)
                    a[i++] = a[j];

            while (i < a.Length)
                a[i++] = 0;

        }

        static void Main(string[] args)
        {

            while (true)
            {

                Console.Write("Enter number of elements (0 to exit): ");
                int n = int.Parse(Console.ReadLine());

                if (n == 0)
                    break;

                int[] a = CreateArray(n);

                Print(a);
                MoveZeros(a);
                Print(a);
                Console.WriteLine();

            }

        }
    }

}

When the application is run, it produces output like this:

            
Enter number of elements (0 to exit): 1
 0
 0

Enter number of elements (0 to exit): 1
 2
 2

Enter number of elements (0 to exit): 2
 0 1
 1 0

Enter number of elements (0 to exit): 5
 0 2 3 0 5
 2 3 5 0 0

Enter number of elements (0 to exit): 10
 0 0 2 2 4 0 5 1 5 0
 2 2 4 5 1 5 0 0 0 0

Enter number of elements (0 to exit): 20
 2 4 0 1 5 0 3 4 4 5 3 1 5 0 0 4 5 3 5 4
 2 4 1 5 3 4 4 5 3 1 5 4 5 3 5 4 0 0 0 0

Enter number of elements (0 to exit): 0
                
    

Discussion

In this exercise we have seen one seemingly abstract problem. But that doesn't have to be that way. Imagine a messaging system in which a number of messages arrive for processing. The task could be to move all messages with empty payload to the end of the queue, so that messages carrying actual payload have precedence. Such request would then be almost identical to this exercise.

While solving theoretical problems, it is very important to keep the practical perspective. Virtually every theoretical problem can appear in practice, often obscured by the boring implementation details of the system at hand. Our ability to separate the core problem from implementation details may then be of great importance when searching for the efficient solution.

---