Finding Minimum Weight Path Through Matrix

by Zoran Horvat
May 21, 2015

Problem Statement

A matrix of integer numbers is given, each cell representing a weight. Write a function which finds a continuous path connecting any element of the first row with any element of the last row in the matrix, such that the sum of elements along the path is minimized. Function should receive a matrix and return

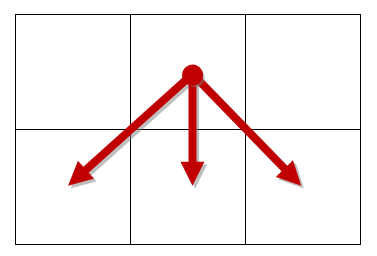
When matrix is drawn in a usual way, path walks strictly downwards through it. From each cell it is legal to move to one of the three cells directly beneath it, as shown in the following picture.

For example, take a look at the following matrix:

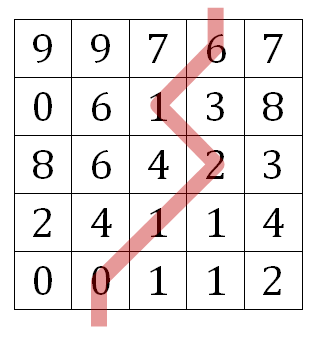
The red line is laid over the minimum weight path. Sum of weights on this path is 10. For this particular matrix, the function should return array [4, 3, 4, 3, 2], because the path consists of elements in locations (1, 4), (2, 3), (3, 4), (4, 3) and (5, 2). Note that 1-based row and column indices are used.

Problem Analysis

Despite the somewhat boring statement, this problem occurs quite often in real life. A walker could try to find the path through tall grass, such that the grass is shortest along the selected route. The problem is also similar to the lightning effect. Roughly speaking, lightning finds the lowest resistance path from the cloud towards the earth.

We can approach this problem incrementally. How would it go if the matrix only had one row? In that case, the minimum weight path would be the minimum weight element from the first row.

How would it go if we added one additional row? In that case, we could find minimum path to a given element in the second row by finding the lowest value in the first row and then just stepping to the second row from that element.

And so the analysis goes on by adding more and more rows to the matrix, until the matrix is fully populated. The result of this operation is another matrix, fully populated by minimum weights of paths to each of the elements.

Picture below shows two matrices. The one on the left is the matrix of weights. The one on the right is populated by calculating minimum path weight to each of the cells. As you can see, many paths die out because a better candidate appears down along the way. In the end, one path prevails, having minimum total weight, and that path will be produced as the result of the algorithm.

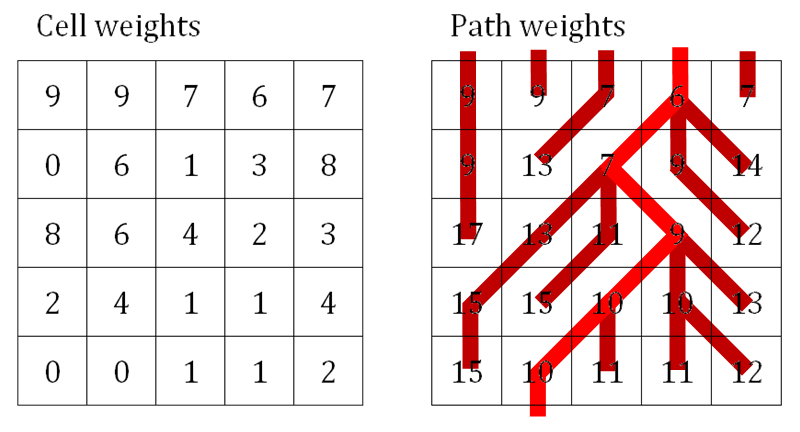
After the path weights matrix is built, we can find the minimum value on the last row. That value – 10 in the example above – will indicate the weight of the winning path. It still doesn’t tell us which elements fall on the path. At that point, we can look at the elements right above the winning element and see from which element we could arrive to the winner in order to reach its weight. In the example above, that is another element with path weight 10. We continue further, moving up the matrix and finding predecessors for each of the elements, until the first row is hit. At that point we will have the full path reconstructed.

Time required to traverse the matrix and build minimum weight paths matrix is proportional to number of elements in the matrix. Time required to figure out the minimum weight path consists of two steps. In the first step we are finding the winning element in the last row, which takes time proportional to number of columns. The second step is to backtrack the winning elements until we reach the first row in the matrix, which requires time proportional to number of rows of the matrix.

Total time of the algorithm is then O(MN + M + N) = O(MN), where M and N are dimensions of the matrix.

Solution

Here is the function which accepts the weights matrix and builds the path weights matrix:

function BuildPathWeights(weights, rowsCount, colsCount)
    -- weights – matrix containing weights
    -- rowsCount – total number of rows in the matrix
    -- colsCount – total number of columns in the matrix
    -- returns matrix with path weights
begin

    pathWeights = new matrix rowsCount x colsCount

    for col = 1 to colsCount
        pathWeights(1, col) = weights(1, col)

    for row = 2 to rowsCount
        begin

            for col = 1 to colsCount
                begin

                    candidateCol = col

                    if col > 1 AND
                       pathWeights(row – 1, col – 1) < pathWeights(row – 1, candidateCol) then
                       candidateCol = col - 1

                    if col < colsCount AND
                       pathWeights(row - 1, col + 1) < pathWeights(row - 1, candidateCol) then
                           candidateCol = col + 1

                    pathWeights(row, col) = pathWeights(row - 1, candidateCol) + weights(row, col)

                end

        end

    return pathWeights;

end

This function simply walks through the matrix, row-wise. In each cell it visits it has up to three candidate cells right above from which the minimum weight path could arrive to the current cell. The function simply chooses the best fit candidate and sets minimum weight path for the current cell.

Once the path weights matrix if built, we can reconstruct the minimum weight path through the whole matrix. That is what the next function does:

function ExtractMinimumWeightPath(weights, pathWeights, rowsCount, colsCount)
    -- weights – matrix of weights
    -- pathWeights – matrix produced by BuildPathWeights function
    -- rowsCount – number of rows in the matrix
    -- colsCount – number of columns in the matrix
begin

    path = new array with rowsCount elements
    col = 1
    for i = 2 to colsCount
        if (pathWeights(rowsCount, i) < pathWeights(rowsCount, col) then
            col = i

    row = rowsCount

    repeat

        path(row) = col

        if col > 1 AND
            pathWeights(row – 1, col – 1) + weights(row, col) = pathWeights(row, col) then
            col = col – 1
        else if col < colsCount AND
            pathWeights(row – 1, col + 1) + weights(row, col) = pathWeights(row, col) then
            col = col + 1

        row = row - 1

    until row = 0

    path(1) = col

    return path;

}

At the beginning, this function first identifies the overall winner – the element of the last row which has the lowest path weight. After that, the function backtracks the minimum weight path until the first row is reached.

In the end, it only remains to tie these two functions together into a working solution:

function GetMinimumPath(weights, rowsCount, colsCount)
    -- weights – matrix with weights
    -- rowsCount – number of rows in the matrix
    -- colsCount – number of columns in the matrix
begin

    pathWeights = BuildPathWeights(weights, rowsCount, colsCount)
    path = ExtractMinimumWeightPath(weights, pathWeights, rowsCount, colsCount)

    return path

end

This function simply delegates work to the two specialized functions we have prepared earlier. Net result is the array containing column indices from the minimum weight path, as requested in the problem statement.

Implementation

Below is the complete console application implementation in C# which solves the problem of finding minimum weight path through the matrix.

using System;

namespace MinWeightPath
{

    class Program
    {

        static Random rnd = new Random();

        static int[,] InitializeMatrix(int n, int m)
        {

            int[,] matrix = new int[n, m];

            for (int i = 0; i < n; i++)
                for (int j = 0; j < m; j++)
                    matrix[i, j] = rnd.Next(10);

            return matrix;

        }

        static int[] GetMinimumPath(int[,] weights)
        {

            int[,] pathWeights = BuildPathWeights(weights);
            int[] path = ExtractMinimumWeightPath(weights, pathWeights);

            return path;

        }

        private static int[,] BuildPathWeights(int[,] weights)
        {

            int rowsCount = weights.GetLength(0);
            int colsCount = weights.GetLength(1);

            int[,] pathWeights = new int[rowsCount, colsCount];

            for (int i = 0; i < colsCount; i++)
                pathWeights[0, i] = weights[0, i];

            for (int row = 1; row < rowsCount; row++)
            {
                for (int col = 0; col < colsCount; col++)
                {

                    int candidateCol = col;

                    if (col > 0 &&
                        pathWeights[row - 1, col - 1] < pathWeights[row - 1, candidateCol])
                        candidateCol = col - 1;

                    if (col < colsCount - 1 &&
                        pathWeights[row - 1, col + 1] < pathWeights[row - 1, candidateCol])
                        candidateCol = col + 1;

                    pathWeights[row, col] = pathWeights[row - 1, candidateCol] + weights[row, col];

                }
            }

            return pathWeights;

        }

        private static int[] ExtractMinimumWeightPath(int[,] weights, int[,] pathWeights)
        {

            int rowsCount = weights.GetLength(0);
            int colsCount = weights.GetLength(1);

            int[] path = new int[rowsCount];

            int col = 0;
            for (int i = 1; i < colsCount; i++)
                if (pathWeights[rowsCount - 1, i] < pathWeights[rowsCount - 1, col])
                    col = i;

            int row = rowsCount - 1;
            do
            {

                path[row] = col + 1;

                if (col > 0 &&
                    pathWeights[row - 1, col - 1] + weights[row, col] == pathWeights[row, col])
                    col = col - 1;
                else if (col < colsCount - 1 &&
                    pathWeights[row - 1, col + 1] + weights[row, col] == pathWeights[row, col])
                    col = col + 1;

                row--;

            }
            while (row > 0);

            path[0] = col + 1;

            return path;

        }

        static void PrintPath(int[,] matrix, int[] path)
        {

            int rowsCount = matrix.GetLength(0);
            int colsCount = matrix.GetLength(1);

            int sum = 0;


            for (int row = 0; row < rowsCount; row++)
            {

                Console.WriteLine();

                for (int col = 0; col < colsCount; col++)
                {

                    string prefix = " ";
                    string suffix = " ";

                    if (col == path[row] - 1)
                    {

                        sum += matrix[row, col];

                        prefix = "[";
                        suffix = "]";

                    }

                    Console.Write(" {0}{1}{2} ", prefix, matrix[row, col], suffix);

                }

            }

            Console.WriteLine();
            Console.WriteLine();
            Console.WriteLine("Sum of weights: {0}", sum);
            Console.WriteLine();

        }

        static void Main(string[] args)
        {

            while (true)
            {

                Console.Write("Enter number of rows (0 to exit): ");
                int rowsCount = int.Parse(Console.ReadLine());

                if (rowsCount <= 0)
                    break;

                Console.Write("Enter number of columns: ");
                int colsCount = int.Parse(Console.ReadLine());

                int[,] matrix = InitializeMatrix(rowsCount, colsCount);

                int[] path = GetMinimumPath(matrix);

                PrintPath(matrix, path);

            }

        }
    }
}

Demonstration

When console application listed above is run, it produces the following output:

            
Enter number of rows (0 to exit): 3
Enter number of columns: 5

  9    7    8   [3]   8
  8    6   [1]   2    3
  4    7    5   [0]   8

Sum of weights: 4

Enter number of rows (0 to exit): 5
Enter number of columns: 7

  6    4    8    9    1   [0]   3
  3    0    5    9   [3]   4    2
  3    0    8    1   [1]   3    3
  4    2    0    7   [0]   9    3
  7    5    9    9    3   [0]   3

Sum of weights: 4

Enter number of rows (0 to exit): 5
Enter number of columns: 10

  5    1    6    4    9    8   [0]   3    0    1
  8    4    7    2    8    4   [2]   5    3    7
  6    7    7    2    9    6    6   [0]   8    4
  3    2    2    6    1    9    4   [2]   6    7
  2    8    0    7    6    6    6   [1]   2    9

Sum of weights: 5

Enter number of rows (0 to exit): 10
Enter number of columns: 10

  1    8    1    7    6   [1]   2    5    8    6
  9    6    6    4    8   [2]   7    1    4    0
  1    1    9    5   [0]   7    8    6    9    7
  8    5    5    8   [1]   3    7    3    3    8
  1    8    9    3   [2]   6    4    0    5    6
  7    0    9    3    0   [0]   9    5    7    8
  2    5    6    0    7    3   [0]   8    3    4
  5    4    7    6    9    3   [1]   5    3    4
  2    8    1    2    9    8    5   [2]   7    1
  4    1    6    4    6    5   [1]   9    5    8

Sum of weights: 10

Enter number of rows (0 to exit): 20
Enter number of columns: 10

  3    2    9    2    9   [0]   6    9    4    1
  8    7    8    5    9   [0]   4    4    3    0
  9    4    6    2    7   [3]   4    4    5    2
  0    7    0    8    5    6   [2]   9    2    2
  5    7    5    8    3    2   [0]   5    8    4
  6    2    5    9    5    9   [6]   6    4    5
  5    1    4    2    1   [0]   7    0    0    3
  8    4    1    1    5   [2]   8    7    8    5
  3    9    5    0    6    7   [2]   1    2    6
  0    5    4    6    6   [3]   3    3    7    2
  4    0    4    4    6   [1]   0    4    3    3
  0    8    7    9   [2]   5    6    3    5    3
  8    6    7    3    3   [2]   9    5    4    1
  8    5    0    6   [0]   3    5    0    4    4
  7    7    7    8    6   [1]   8    5    4    1
  7    9    7    3   [4]   8    2    1    1    4
  2    5    0   [1]   4    4    8    1    8    9
  0    5    9   [0]   6    0    8    9    7    2
  4    4   [0]   3    4    9    7    6    2    2
  1   [4]   9    9    2    1    7    5    3    1

Sum of weights: 33

Enter number of rows (0 to exit): 0
                
    

---