Finding Maximum Value in Queue

by Zoran Horvat
February 16, 2021

Problem Statement

Implement a queue structure which exposes operations: Enqueue, which adds an element to the end; Dequeue, which removes an element from the beginning; and GetMaxValue, which returns maximum value currently stored in the queue, without removing it. Each time current maximum is dequeued, the queue’s GetMaxValue operation should reflect the new largest element that has retained.

Example: Below is a sequence of enqueue/dequeue operations on a queue which is initially empty. In each step, state of the queue and maximum value (which would be returned by GetMaxValue) are indicated.

enqueue 3   [3]            max=3
enqueue 5   [3, 5]         max=5
enqueue 2   [3, 5, 2]      max=5
enqueue 4   [3, 5, 2, 4]   max=5
dequeue 3   [5, 2, 4]      max=5
enqueue 1   [5, 2, 4, 1]   max=5
dequeue 5   [2, 4, 1]      max=4
dequeue 2   [4, 1]         max=4
dequeue 4   [1]            max=1

Problem Analysis

If the queue were only to implement adding items (the Enqueue operation), finding maximum of values stored in the queue would be straight-forward. We would maintain current maximum value and update it with every new element added.

Enqueue(x)
  if queue_is_empty OR x > current_max
    current_max = x
  -- add x to the end

As more items are added to the queue, the current_max value would track maximum out of all values seen so far.

However, there is the culprit, the Dequeue operation, which can remove current maximum, or leave it in the queue, depending on whether the largest value has travelled all the way to the beginning, or it is still stored somewhere behind in the queue. Unfortunately, we don’t know which of the two had happened, even in cases when the dequeued value equals the current maximum. Observe the following order of operations, for an example when dequeuing the maximum value doesn’t change the overall maximum.

enqueue 2   [2]         max=2
enqueue 1   [2, 1]      max=2
enqueue 2   [2, 1, 2]   max=2
dequeue 2   [1, 2]      max=2

Even though the Dequeue result equals current maximum, the maximum value has remained, because there is another instance of value 2 remaining in the queue. Therefore, it looks like we should somehow refresh maximum, at least in situations when dequeued value equals previous maximum. That is to say that we don’t have to refresh current maximum when dequeued value is smaller – in that case, it is obvious that the largest value is still somewhere in the queue.

Dequeue()
  output = DequeueInternally()
  if output == current_max
    current_max = RecalculateMaximum()

While this implementation would certainly work, the problem is with efficiency. The RecalculateMaximum operation apparently has no idea where the next maximum could be located, and therefore must pass through all the items remaining in queue to find the one that is largest among them. That operation looks to take time proportional to number of elements currently residing in the queue. Could we do better?

It is common in software engineering to solve such problems by designing a data structure which can efficiently serve the result we need.

In this exercise, we conclude that a common queue, which we imagine as a linear structure of consecutive items, is not appropriate, because it doesn’t guarantee efficient calculation of the next maximum value when we need it. We shall now focus on implementing a specialized data structure which solves the efficiency problem.

Prospect of Using Stacks as Queues

Queue is the FIFO structure – first-in, first-out – and that has caused issues in this exercise, because FIFO structure is notoriously bad at propagating information backwards. We want the information about candidates for new maximum readily available, but that information is stored behind the head element, and not readily available. That is where it becomes apparent that FIFO structures cannot propagate information backwards efficiently.

However, LIFO structure – last-in, first-out – also known as stack, is a perfect match for the problem of backpropagating information. As each item is pushed to the stack, a piece of its information can be retained aside, to affect other elements that will be pushed later, when this element is already deep under the top.

Potential to solve the problem of calculating maximum among remaining elements is there, and we only need to solve the problem of turning LIFO structure into FIFO structure. To address that issue, we remember that if we pass items through two LIFO structures in succession, their order would be reverted twice, and therefore retained – two stacks can be used as a queue, and now we shall construct the data structure based on that idea.

Implementing Queue via Two Stacks

We could place two queues next to each other. The one on the left would accept new elements passed to Enqueue, and the one on the right would serve elements when Dequeue is called. However, being stacks, both can maintain the running maximum, i.e., each element can maintain the maximum of itself and any items below it. Therefore, the stacks would store pairs of values (item, running_max). Topmost element in each stack would indicate the maximum of all items in that stack. Combination of two maximums is therefore the overall maximum in the entire structure.

First things first, the following picture shows state of both stacks after four items were enqueued: 3, 5, 2 and 4, in that order.

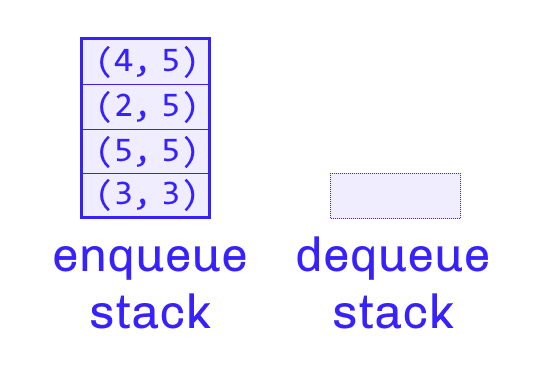
As each value is pushed to the left-hand stack, and the running maximum is recalculated along the way (the second item in the pair). If the caller wanted to know current maximum, that would be 5, because top-most item is indicating maximum value 5. That is when Dequeue is called for the first time, and we must procure the first item that was enqueued.

Stack on the left is offering items, but in the reverse order. We need to reverse them once more before we can get grasp of the first element that was enqueued. That is where the right-hand stack comes to the picture.

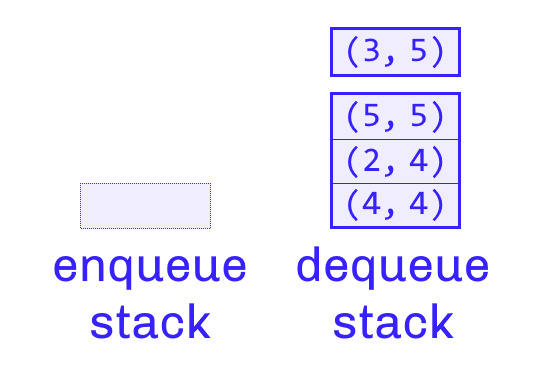
If the right stack is empty, then we shall pop all pairs from the left stack and push them to the right stack. After that, we can simply pop one element from the right stack, as the first item added to the structure. That is the process shown in the picture below.

Note, however, that the running maximum is recalculated through this process. That is precisely how this data structure works. Every dequeue which causes items to be pushed to the right stack will cause the maximum of all elements that remain in the queue to be recalculated on the fly. Overall maximum will then be readily available.

As the final demonstration, we can see what will change when another value is enqueued. That value would be pushed to the left queue, and it will contribute to the maximum calculation as usual.

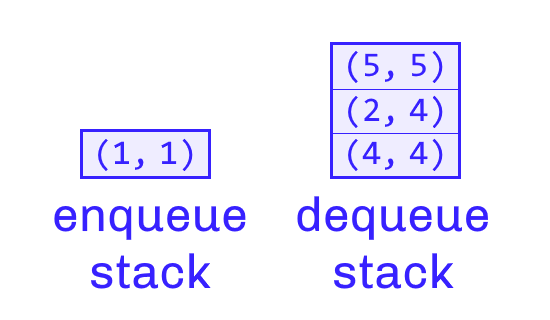
Picture below shows typical state that appears after a few Enqueue and Dequeue operations, where both stacks are non-empty. Maximum is then calculated by taking the larger of the two maximums from top pairs of each stack. In the picture below, that is maximum of 1 and 5, which is, of course, 5.

This has demonstrated that we can apply two stacks to implement a queue which serves maximum value at immediate notice. Before implementing this structure, we shall analyze its performance, so that we can assess how efficient it is compared to a common queue.

Performance Analysis

We can start from the viewing point of a single item which passes through the whole lifecycle of being enqueued, then being silently transferred to the right stack, until it is finally dequeued and removed from the data structure altogether.

Total cost of passing one item through the queue is then: two times push and pop (first to left stack, and then to right stack), and two comparisons to calculate the running maximum. That is the grand total of operations we perform per one item enqueued and eventually dequeued from the queue. We find, therefore, that enqueue and dequeue operations average O(1) cost. For a sequence of N items that are passed through the queue during an entire operation, we see that the queue will operate in O(N) time.

The trouble is that this calculation is only correct at average. True behavior of this structure is that we shall pay only half the price at almost every enqueue or dequeue operation, leaving the other half for a later occasion. That occasion will happen when dequeue stack is empty, and at that moment we shall pay the remaining half of the cost for all items currently residing in the queue. That may at times be quite expensive, causing program to look like frozen for a period of time. Please keep this issue in mind and assess whether that is acceptable in whatever problem domain you plan to apply this algorithm.

It is a bit easier to assess performance of the GetMaxValue operation because it boils down to comparing running maximums from tops of the two stacks. That is obviously an O(1) operation.

Space complexity is also easy to assess. Each item is only stored once in either of the stacks, and it is accompanied by exactly one running maximum. Since stacks take space proportional to size of items they store, we conclude that this data structure requires O(M) space, where M is number of items concurrently residing in the queue.

Therefore, we conclude that queue constructed with use of two stacks exhibits O(1) time complexity on average for all operations: Enqueue, Dequeue and GetMaxValue. Overall complexity of passing N items through the queue is O(N). Overall space complexity when M items are concurrently stored in queue is O(M). That leaves little room for improvement.

Implementing the Queue with Maximum

Below is the entire implementation of the queue structure in C#. It is based on standard Stack class. It is also a constrained generic class, which means that it can be applied to any type of items, guaranteed that they can be compared in order to choose the larger of the two.

Class below is following common .NET rules, which means that it has a few additional methods besides those that were requested. The GetMaxValue method is implemented as the Max property, once again following common .NET practice.

Code is telling more than words, so here is the entire queue implementation.

using System;
using System.Collections;
using System.Collections.Generic;
using System.Linq;

namespace Demo
{
  public class MaxQueue<T> : IEnumerable<T>
    where T : IComparable<T>
  {
    private Stack<(T item, T max)> EnqueueStack { get; } =
      new Stack<(T item, T max)>();

    private Stack<(T item, T max)> DequeueStack { get; } =
      new Stack<(T item, T max)>();

    public int Count =>
      this.EnqueueStack.Count +
      this.DequeueStack.Count;

    public void Enqueue(T item) =>
      this.Push(item, this.EnqueueStack);

    public T Dequeue()
    {
      if (this.Count == 0)
        throw new InvalidOperationException();

      this.EnsurePopAvailable();
      return this.DequeueStack.Pop().item;
    }

    public T Max =>
      this.EnqueueStack.Count > 0 &&
      this.EnqueueStack.Peek().max is T leftMax
        ? this.GetMax(leftMax)
        : this.GetRightMax();

    private T GetMax(T left) =>
      this.DequeueStack.Count > 0 &&
      this.DequeueStack.Peek().max is T right &&
      right.CompareTo(left) > 0
        ? right
        : left;

    private T GetRightMax() =>
      this.DequeueStack.Count > 0
        ? this.DequeueStack.Peek().max
        : throw new InvalidOperationException();

    private void Push(T item, Stack<(T item, T max)> stack)
    {
      T max =
        stack.Count > 0 &&
        stack.Peek() is (T _, T prevMax) &&
        prevMax.CompareTo(item) > 0
          ? prevMax
          : item;

      stack.Push((item, max));
    }

    private void EnsurePopAvailable()
    {
      if (this.DequeueStack.Count == 0)
      {
        this.PourIntoDequeueStack();
      }
    }

    private void PourIntoDequeueStack()
    {
      while (this.EnqueueStack.TryPop(out (T item, T _) tuple))
      {
        this.Push(tuple.item, this.DequeueStack);
      }
    }

    public IEnumerator<T> GetEnumerator() =>
      this.DequeueStack
        .Concat(this.EnqueueStack.Reverse())
        .Select(tuple => tuple.item)
        .GetEnumerator();

    IEnumerator IEnumerable.GetEnumerator() =>
      this.GetEnumerator();

    public override string ToString() =>
      "[" +  string.Join(", ", this.StringItems) + "]";

    private IEnumerable<string> StringItems =>
      this.Select(item => item.ToString());
  }
}

Demonstrating Implementation

Below is a console program which supplies sample values to the MaxQueue<int>, reporting content and maximum values returned by the queue after each operation.

using System;

namespace Demo
{
  static class Program
  {
    static void Main(string[] args)
    {
      new MaxQueue<int>()
        .ReportEnqueue(3)
        .ReportEnqueue(5)
        .ReportEnqueue(2)
        .ReportEnqueue(4)
        .ReportDequeue()
        .ReportEnqueue(1)
        .ReportDequeue()
        .ReportDequeue()
        .ReportDequeue();

      Console.Write("Press ENTER to exit . . . ");
      Console.ReadLine();
    }

    static MaxQueue<int> ReportEnqueue(
      this MaxQueue<int> queue, int value)
    {
      queue.Enqueue(value);
      Report("enqueue", value, queue);
      return queue;
    }

    static MaxQueue<int> ReportDequeue(
      this MaxQueue<int> queue)
    {
      int value = queue.Dequeue();
      Report("dequeue", value, queue);
      return queue;
    }

    static void Report(
      string operation, int value, MaxQueue<int> queue) =>
      Console.WriteLine(
        $"{operation,7} {value}   {queue,-12}   max={queue.Max}");
  }
}

When this code is run, it prints the same content as in the example stated at the beginning of this exercise.

enqueue 3   [3]            max=3
enqueue 5   [3, 5]         max=5
enqueue 2   [3, 5, 2]      max=5
enqueue 4   [3, 5, 2, 4]   max=5
dequeue 3   [5, 2, 4]      max=5
enqueue 1   [5, 2, 4, 1]   max=5
dequeue 5   [2, 4, 1]      max=4
dequeue 2   [4, 1]         max=4
dequeue 4   [1]            max=1

This completes implementation of the queue structure which can report maximum item at any time, while only spending constant time to calculate it.

Conclusion

In this exercise, we have investigated one possible implementation of the queue structure, which guarantees to calculate maximum of contained items in constant time on average, while retaining constant-time average for enqueuing and dequeuing operations.

Success in solving this problem is underlying one general principle: That performance of systems can be tweaked by the choice of data structures. When we encounter a performance issue, we turn attention to investigating specialized data structures which are guaranteeing better performance right where we need it.

---