Finding Arithmetic Expression to Construct a Value from Given Numbers
by Zoran Horvat
Problem Statement
Goal of this exercise is to write code which accepts a set of numbers and then tries to devise an arithmetic expression that yields a requested value, using four basic arithmetic operations: addition, subtraction, multiplication and division. Each input number must be used exactly once in the expression. Division is applicable only to numbers that are divisible without remainder. All input numbers and the target number are integers greater than zero. There are no more than 5 input numbers and target number is not larger than 1000.
Example 1: Suppose that numbers 4, 8 and 9 are given and value 18 should be constructed. One solution is: 9 * 8 / 4.
Example 2: If numbers 6, 7 and 9 are given, number 3 requested, then solution is: 6 / (9 - 7).
Problem Analysis
We can approach this problem in bottom-up fashion: start from input numbers and then combine them into larger and larger expressions. Each expression that is reached can be combined further. For each expression list of participating input numbers participating is maintained. Two expressions can be combined only if their lists are disjoint - one input number can be used at most in one of the expressions.
Combining two expressions actually means to apply all operators that are applicable. Basically, addition, subtraction and multiplication can always be applied. Only division is questionable - it is applicable only if results of two expressions can be divided without remainder. Addition and multiplication are commutative (a+b=b+a and a*b=b*a), meaning that order of operand is not important. Subtraction and division are not commutative, meaning that they can be applied in two different ways for each pair of expressions. Consequently, we have a total of six possible operations that can be applied to any pair of expressions. In other words, one pair of expressions can be expanded into up to six other expressions. For example, suppose that values 3 and 6 are available. These two values can produce: 3+6=9, 3-6=-3, 6-3=3, 3*6=18 and 6/3=2 - total of five new values. We cannot divide 3 by 6 using integer division. Even more, we can reject expression 3-6=-3 because it can always be reached in the opposite direction - by subtracting the result of expression 6-3=3 from any other expression.
By this point we have decided how to construct larger expressions from smaller ones. But now we have a problem of a different sort: there are results that can be constructed from same set of numbers in more than one way. For example, if there are numbers 2 and 2, we can create number 4 as 2+2 or 2*2. It could be a serious problem should we repeat all subsequent calculations for the second form. Number of multiple paths that lead to the same value would quickly start to build up. Take a similar example, numbers: 1, 2 and 3. These numbers can produce value 5 in quite a few ways: 2*1+3, 2/1+3, 2+3*1, 2+3/1, 2*3-1. There must be a way to detect that these three numbers were employed to reach value 5 (e.g. like 2*1+3) and then to discard all subsequent solutions to the same problem. So the next element of the solution is to make sure that all values produced are remembered in a kind of a cache, all in order to discard further solutions to the same partial problem. But note that expressions 2+3=5 and 2*1+3=5 are different: they differ in numbers that are used to construct them. Generally, two expressions are considered the same (in terms that they carry the same information) if they have the same lists of input numbers and produce the same value.
Next issue to discuss is how does the algorithm proceed. It is obvious that existing expressions are producing new expressions that are simply added to the set of all valid expressions. Now we need to decide on order in which expressions are going to be combined so to guarantee that all pairs of expressions are combined before the algorithm completes. One way to introduce such a guarantee is to maintain a queue of expressions that have not been processed, i.e. paired with other expressions. In each step of the algorithm, an expression is dequeued, then combined with all existing expressions (possibly producing new expressions that are not equal to any existing expression), and only then added to the set of all valid expressions. In this way, it is guaranteed that any pair of expressions is picked up for expansion, consequently providing a guarantee that all pairs of expressions will be combined before the end of the execution. Should there be a valid solution, it will certainly be found.
Final question to answer is about starting conditions. When algorithm commences, set of valid expressions consists of input values - each value is a valid expression on its own right. So if we have a set of four input values, then we begin with four valid expressions. At the same time, all four expressions are added to the queue of expressions to process. That is the state in which algorithm starts to unfold.
Complete algorithm that solves the problem is now very simple:
E - set of all valid expressions
Q - queue of expressions that have not been expanded yet
N - set of input numbers
v - target value
Goal: To create an expression N->v, which uses all numbers from N to produce value v
for all numbers n in N
Add expression n->n to Q
Add expression n->n to E
while Q is not empty and E does not contain expression N->v
begin
e = expression dequeued from Q
for each expression f in E
begin
G = set of expressions obtained by combining e and f
for each expression g in G
if g is not in E then
Enqueue g to Q
Add g to E
end
end
if E contains expression N->v then
print expression N->v
Implementation
Now that we have decided on algorithm that solves the problem, we need to discuss implementation details. Namely, we have to answer the following questions:
- How do we express the arithmetic expression?
- How do we check whether expression has already been generated?
- How do we combine two expressions to create more expressions?
- How do we add expressions to the set and to the queue?
In each of these segments there can be many viable solutions. Generally, the simpler the better. Answer to first question, how to represent an expression, can be as follows. Each expression is defined recursively by pointing to two expressions that represent left and right operand and by specifying the operation applied to the two. In addition, expression carries its value (which is generally redundant, but quite useful to avoid constant re-evaluation of all expressions during algorithm execution). One more redundant information comes handy: a list of input numbers used to construct the expression (this list is redundant because it can be constructed recursively by joining corresponding lists of the operand expressions). Recursion stops at input numbers - each number is treated as an expression which does not have operands or operation - number defines its value and it is the sole element in the list of numbers used.
Second issue deals with identifying expressions. As already explained above, two expressions are considered equal if they share the same set of input numbers and have the same value when calculated. This leads to an idea that input numbers could be remembered as a bit-mask which would then be combined with expression value. Each bit in the mask indicates whether corresponding input number participates in the expression. This is the point when an example would come handy. Let input numbers be 1, 2, 3, 4 and expression 2*1+3=5 should be encoded. Numeric code which corresponds with this expression is shown on the following picture.
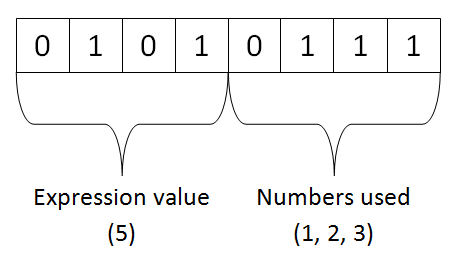
Lower four bits of the number are dedicated to input numbers - three bits one indicate that corresponding numbers (1, 2 and 3) are participating in the expression, while fourth bit zero indicates that the remaining input number (4) does not take place in this expression. Bits above the fourth position contain value obtained when expression is evaluated (5 in this case). Note that expression 2/1+3=5 has the same signature, and that is exactly what we wanted to obtain.
Next question is the one about combining expressions. Two arbitrary expressions can be combined only if their input numbers sets are disjoint. In example above, input numbers are indicated by lowest four bits in the expression code. Hence the solution - lowest bits of the two expressions codes must be disjoint (bitwise AND operation produces all zeros). After testing whether two expressions can be combined in the first place, next operation is to actually combine them. We have already explained that there are six possible arithmetic operations that can be applied to any pair of expressions. Solution to the problem is simply to try all of them and to produce up to six new expressions. Any expression generated would have a value that is determined by input expressions' values and the operation applied. Masks indicating input numbers should be combined into one mask (bitwise OR operation). That would naturally lead to creating a signature of the new expression. Off course, new expression would have to point to original expressions as its left and right operand.
Final question is about maintaining a set and a queue of expressions. At this step it becomes obvious why we had to devise expression signatures. With that tool at hand, we can create an array of whatever values we need and then simply use expression signature as an index pointing to the corresponding value in the array. The queue would be maintained equally simply - it would contain just expression signatures, since the signature is quite sufficient to access all the information about the expression.
Now that all technical difficulties have been dealt with, we are ready to provide the full source code of the solution. The source code is commented so that it can be read apart from the algorithm provided above. It is given in the form of C# console application which depends on a couple of .NET Framework classes (hashtable, dictionary, queue). But these classes are only collections with well known behavior, meaning that you could rewrite the solution to any other programming language or framework easily.
using System;
namespace Arithmetics
{
class Program
{
static int[] ReadInput(out int value)
{
Console.Write("Enter integer numbers to use (space-separated): ");
string s = Console.ReadLine();
string[] parts = s.Split(new char[] { ' ' }, StringSplitOptions.RemoveEmptyEntries);
int[] a = new int[parts.Length];
for (int i = 0; i < a.Length; i++)
a[i] = int.Parse(parts[i]);
Console.Write("Enter integer value to calculate: ");
value = int.Parse(Console.ReadLine());
return a;
}
static void SolveAndPrint(int[] numbers, int targetValue)
{
int targetKey = (targetValue << numbers.Length) + (1 << numbers.Length) - 1;
// (value << numbers.Length) represents expression value
// (1 << numbers.Length) - 1 represents mask with all bits set to 1,
// i.e. mask in which each input number has been used exactly once
// to build the expression.
System.Collections.Generic.HashSet<int> solvedKeys =
new System.Collections.Generic.HashSet<int>();
// Each number in the collection indicates that corresponding value + mask
// has been reached using arithmetical operations.
System.Collections.Generic.Dictionary<int, int> keyToLeftParent =
new System.Collections.Generic.Dictionary<int, int>();
// For each solved key (value + mask), there is an entry indicating
// result of the expression on the left side of the arithmetic
// operator. Missing value indicates that key represents the
// raw number (taken from the input list), rather than
// the result of a calculation.
System.Collections.Generic.Dictionary<int, int> keyToRightParent =
new System.Collections.Generic.Dictionary<int, int>();
// Same as keyToLeftParent, only indicating the right parent
// used to build the expression.
System.Collections.Generic.Dictionary<int, char> keyToOperator =
new System.Collections.Generic.Dictionary<int, char>();
// Indicates arithmetic operator used to build this node
// from left and right parent nodes. Missing value for a given key
// indicates that key is a raw value taken from input array,
// rather than result of an arithmetic operation.
System.Collections.Generic.Queue<int> queue =
new System.Collections.Generic.Queue<int>();
// Keys (value + mask pairs) that have not been processed yet
// First step is to initialize the structures:
// Add all input values into corresponding array entries and
// add them to the queue so that the operation can begin
for (int i = 0; i < numbers.Length; i++)
{
int key = (numbers[i] << numbers.Length) + (1 << i);
solvedKeys.Add(key);
queue.Enqueue(key);
}
// Now expand entries one at the time until queue is empty,
// i.e. until there are no new entries populated.
// Additional stopping condition is that target key has been generated,
// which indicates that problem has been solved and there is no need to
// expand nodes any further.
while (queue.Count > 0 && !solvedKeys.Contains(targetKey))
{
int curKey = queue.Dequeue();
int curMask = curKey & ((1 << numbers.Length) - 1);
int curValue = curKey >> numbers.Length;
// Now first take a snapshot of all keys that
// have been reached because this collection is going to
// change during the following operation
int[] keys = new int[solvedKeys.Count];
solvedKeys.CopyTo(keys);
for (int i = 0; i < keys.Length; i++)
{
int mask = keys[i] & ((1 << numbers.Length) - 1);
int value = keys[i] >> numbers.Length;
if ((mask & curMask) == 0)
{ // Masks are disjoint, i.e. two entries do not use
// the same input number twice.
// This is sufficient condition to combine the two entries
for (int op = 0; op < 6; op++)
{
char opSign = '\0';
int newValue = 0;
switch (op)
{
case 0: // Addition
newValue = curValue + value;
opSign = '+';
break;
case 1: // Subtraction - another value subtracted from current
newValue = curValue - value;
opSign = '-';
break;
case 2: // Subtraction - current value subtracted from another
newValue = value - curValue;
opSign = '-';
break;
case 3: // Multiplication
newValue = curValue * value;
opSign = '*';
break;
case 4: // Division - current divided by another
newValue = -1; // Indicates failure to divide
if (value != 0 && curValue % value == 0)
newValue = curValue value;
opSign = '';
break;
case 5: // Division - other value divided by current
newValue = -1; // Indicates failure to divide
if (curValue != 0 && value % curValue == 0)
newValue = value curValue;
opSign = '';
break;
}
if (newValue >= 0)
{ // Ignore negative values - they can always be created
// the other way around, by subtracting them
// from a larger value so that positive value is reached.
int newMask = (curMask | mask);
// Combine the masks to indicate that all input numbers
// from both operands have been used to produce
// the resulting expression
int newKey = (newValue << numbers.Length) + newMask;
if (!solvedKeys.Contains(newKey))
{ // We have reached a new entry.
// This expression should now be added
// to data structures and processed further
// in the following steps.
// Populate entries that describe newly created expression
solvedKeys.Add(newKey);
if (op == 2 || op == 5)
{ // Special cases - antireflexive operations
// with interchanged operands
keyToLeftParent.Add(newKey, keys[i]);
keyToRightParent.Add(newKey, curKey);
}
else
{
keyToLeftParent.Add(newKey, curKey);
keyToRightParent.Add(newKey, keys[i]);
}
keyToOperator.Add(newKey, opSign);
// Add expression to list of reachable expressions
solvedKeys.Add(newKey);
// Add expression to the queue for further expansion
queue.Enqueue(newKey);
}
}
}
}
}
}
// Now print the solution if it has been found
if (!solvedKeys.Contains(targetKey))
Console.WriteLine("Solution has not been found.");
else
{
PrintExpression(keyToLeftParent, keyToRightParent, keyToOperator, targetKey, numbers.Length);
Console.WriteLine("={0}", targetValue);
}
}
static void PrintExpression(System.Collections.Generic.Dictionary<int, int> keyToLeftParent,
System.Collections.Generic.Dictionary<int, int> keyToRightParent,
System.Collections.Generic.Dictionary<int, char> keyToOperator,
int key, int numbersCount)
{
if (!keyToOperator.ContainsKey(key))
Console.Write("{0}", key >> numbersCount);
else
{
Console.Write("(");
// Recursively print the left operand
PrintExpression(keyToLeftParent, keyToRightParent, keyToOperator,
keyToLeftParent[key], numbersCount);
// Then print the operation sign
Console.Write(keyToOperator[key]);
// Finally, print the right operand
PrintExpression(keyToLeftParent, keyToRightParent, keyToOperator,
keyToRightParent[key], numbersCount);
Console.Write(")");
}
}
static void Main(string[] args)
{
while (true)
{
int value;
int[] numbers = ReadInput(out value);
SolveAndPrint(numbers, value);
Console.Write("More? (y/n) ");
if (Console.ReadLine().ToLower() != "y")
break;
}
}
}
}
Demonstration
When source code provided above is compiled and run, it lets the user pick the input numbers and the desired output number and then attempts to solve the problem, printing out the expression if one is found. Below is the demonstration of our algorithm in action.
Enter integer numbers to use (space-separated): 4 8 9
Enter integer value to calculate: 18
(9*(8/4))=18
More? (y/n) y
Enter integer numbers to use (space-separated): 6 7 9
Enter integer value to calculate: 3
(6/(9-7))=3
More? (y/n) y
Enter integer numbers to use (space-separated): 2 3 4 5
Enter integer value to calculate: 18
(((2*5)-4)*3)=18
More? (y/n) y
Enter integer numbers to use (space-separated): 2 3 4
Enter integer value to calculate: 12
Solution has not been found.
More? (y/n) y
Enter integer numbers to use (space-separated): 1 3 4 6
Enter integer value to calculate: 24
Solution has not been found.
More? (y/n) n
Follow-Up Exercises
Readers are suggested to build upon this solution and work up solutions to extended tasks:
- Print all expressions that produce the requested number, not only the one that utilizes all of the input numbers. Consider example 2,3,4->12 from the demonstration, which does not have the complete solution but does have a simple one: 3*4=12, which omits input value 2.
- If exact solution is not found, then print the solution which is closest to the requested number.
- Extend the solution to support fractional numbers. In the demonstration above, example 1,3,4,6->24 cannot be solved using the algorithm provided, but that problem actually does have a solution when fractional numbers are supported. (Try to figure out the solution before letting the program find it!)
See Also:
If you wish to learn more, please watch my latest video courses

Beginning Object-oriented Programming with C#
In this course, you will learn the basic principles of object-oriented programming, and then learn how to apply those principles to construct an operational and correct code using the C# programming language and .NET.
As the course progresses, you will learn such programming concepts as objects, method resolution, polymorphism, object composition, class inheritance, object substitution, etc., but also the basic principles of object-oriented design and even project management, such as abstraction, dependency injection, open-closed principle, tell don't ask principle, the principles of agile software development and many more.
More...

Design Patterns in C# Made Simple
In this course, you will learn how design patterns can be applied to make code better: flexible, short, readable.
You will learn how to decide when and which pattern to apply by formally analyzing the need to flex around specific axis.
More...

Refactoring to Design Patterns
This course begins with examination of a realistic application, which is poorly factored and doesn't incorporate design patterns. It is nearly impossible to maintain and develop this application further, due to its poor structure and design.
As demonstration after demonstration will unfold, we will refactor this entire application, fitting many design patterns into place almost without effort. By the end of the course, you will know how code refactoring and design patterns can operate together, and help each other create great design.
More...

Mastering Iterative Object-oriented Development in C#
In four and a half hours of this course, you will learn how to control design of classes, design of complex algorithms, and how to recognize and implement data structures.
After completing this course, you will know how to develop a large and complex domain model, which you will be able to maintain and extend further. And, not to forget, the model you develop in this way will be correct and free of bugs.
More...
About

Zoran Horvat is the Principal Consultant at Coding Helmet, speaker and author of 100+ articles, and independent trainer on .NET technology stack. He can often be found speaking at conferences and user groups, promoting object-oriented and functional development style and clean coding practices and techniques that improve longevity of complex business applications.
Elsewhere
Video Courses
- Making Your C# Code More Object-oriented
- Beginning Object-oriented Programming with C#
- Collections and Generics in C#
- Design Patterns in C# Made Simple
- Refactoring to Design Patterns
- Mastering Iterative Object-oriented Programming in C#
- Making Your C# Code More Functional
- Making Your Java Code More Object-oriented
- Writing Purely Functional Code in C#
- Tactical Design Patterns in .NET: Creating Objects
- Tactical Design Patterns in .NET: Control Flow
- Tactical Design Patterns in .NET: Managing Responsibilities
- Advanced Defensive Programming Techniques
- Writing Highly Maintainable Unit Tests
- Improving Testability Through Design
Articles
- Here is Why Calling a Virtual Function from the Constructor is a Bad Idea
- What Makes List<T> So Efficient in .NET?
- Nondestructive Mutation and Records in C#
- Understanding Covariance and Contravariance of Generic Types in C#
- Using Record Types in C#
- Unit Testing Case Study: Calculating Median
- More...