Sum of Squares of First N Numbers

by Zoran Horvat
December 14, 2013

Given a positive number N, write a function which returns sum of squares of numbers between 1 and N, i.e. 1^2 + 2^2 + ... + N^2.

Example: If N is 5, then return value should be 55 (1 + 4 + 9 + 16 + 25 = 55).

Problem Analysis

It is easy to produce sum o squares of a sequence by simply iterating through numbers 1 to N. Here is the function which does precisely that:

function Sum(n)
begin
    sum = 0
    for i = 1 to n
        sum = sum + i * i
    return sum
end

This function runs in O(N) time and O(1) space. In order to improve the running time of the function, we need to find a definite form of the sum of squares. That is possible to do, and here is one of the ways to derive the simple form of the expression:

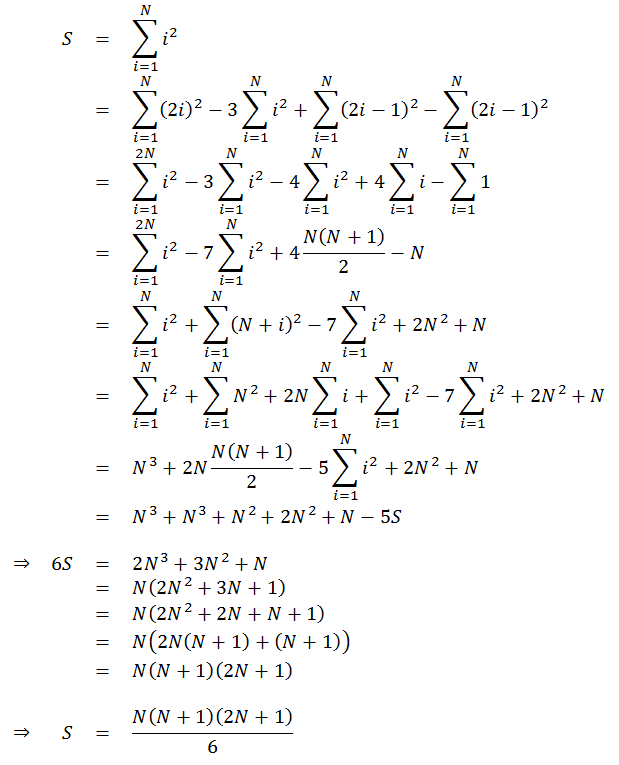
This derivation depends on the equation for calculating simple sum of the numbers 1 to N, which is explained in exercise Sum of First N Numbers . Now the function that runs in O(1) time and O(1) space looks like this:

function Sum(n)
begin
    return n * (n + 1) * (2 * n + 1) / 6
end

Implementation

Below is the full listing of a console application in C# which lets the user enter value N and then prints the sum of squares of the sequence.

using System;

namespace SumOfSquares
{

    public class Program
    {

        static int Sum(int n)
        {
            return n * (n + 1) * (2 * n + 1)  6;
        }


        static void Main(string[] args)
        {

            while (true)
            {

                Console.Write("Enter sequence length (zero to exit): ");
                int n = int.Parse(Console.ReadLine());

                if (n <= 0)
                    break;

                Console.WriteLine("Sum of the sequence is {0}\n", Sum(n));

            }

        }

    }
}

Demonstration

When application is run, it produces output like this:

            
Enter sequence length (zero to exit): 4
Sum of the sequence is 30

Enter sequence length (zero to exit): 5
Sum of the sequence is 55

Enter sequence length (zero to exit): 217
Sum of the sequence is 3429685

Enter sequence length (zero to exit): 0