Best Practices Implementing the IEnumerable Interface
by Zoran Horvat
IEnumerable is one of the most prominent interfaces shipped with the .NET Framework. Nevertheless, in practice we constantly encounter less desired implementations of this interface. In this article we will cover the origin, the purpose, and best practices in implementing IEnumerable interface in C#.
Basics of the Iterator Design Pattern
Iterator pattern is maybe the most frequently used pattern in programming. It lets us solve the problem of iterating through a collection by externalizing the algorithm to a separate class. This is a truly wonderful idea, which goes in line with general motive of design patterns: Identify the changing element and then represent it by its own object.
When talking about collections and iteration through them, the changing element is the process of deciding the next element to visit. But this comes with a twist. The UML class diagram shown below is taken from the Gang of Four book on design patterns. It gives a clear idea what it means to turn the iterating algorithm to an object.
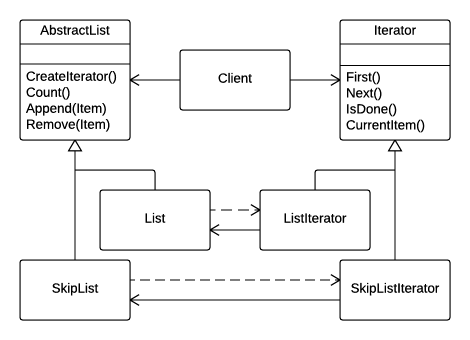
The client in this diagram wishes to talk to abstract lists. It doesn’t want to bother with the details, because details are of no special interest to it when it comes to list implementation. From the client’s point of view, all that matters is traversing the list. And that is precisely where the iterator comes into play, because that is where the traversal algorithm lives.
Without at least some kind of abstract iterator, the client would not be able to traverse the abstract list. Iterator provides the abstract notion of traversal. Then, when concrete list implementation arrives, it comes with the accompanying iterator implementation.
The abstract list in this diagram has an explicit responsibility to provide the iterator object through its CreateIterator() method. This method returns abstract iterator, of course. But the client can use the abstract iterator without having to know anything about its internal organization. As long as there are Next() and IsDone() methods there, the client can traverse the elements. And the CurrentItem() method is there to gain access to actual elements of the list.
This is how it goes with the Iterator pattern in its essence. The problems begin when we try to apply it in C#.
Iterator in C#
.NET Framework defines two important interfaces: IEnumerable and IEnumerator. Mapping to the principal diagram of the Iterator design pattern is clear. IEnumerable is supposed to be implemented by the collection, the AbstractList in the diagram above. This interface defines the GetEnumerator() method, which is called CreateIterator() in the diagram.
IEnumerator interface defines the abstract iterator. It provides such members as the MoveNext() method and Current accessor, for example. These members correspond to Next() and CurrentItem() methods in the diagram.
In that respect, the client could now freely operate at the interface level, leaving the abstract structure even deeper down the hierarchy, as shown in the following diagram.
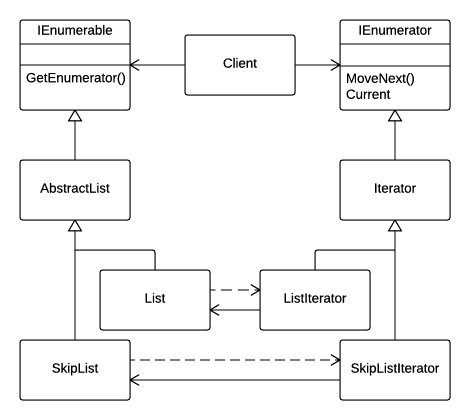
In many cases AbstractList and Iterator base classes would add nothing to the picture and could be entirely removed:
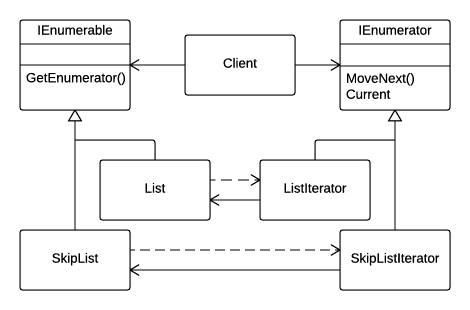
In this organization, concrete lists and their corresponding iterators are implementing the IEnumerable and IEnumerator interfaces directly, reducing the hierarchy to be the same as in the principal diagram.
However attractive this design may look, it hides a few dangers. Basically, this scheme may cause oversimplified implementations in some situations, further leading to shortcomings that cannot be corrected without redesign. In this article we will try to pinpoint the complications that occur if this approach is used as-is in places where not appropriate. We will also try to focus on implementations where this approach is fully satisfactory.
Versioning Content Before Iterating
An important aspect of the Iterator design pattern is that the iterating algorithm is now removed from the collection. Client is free to do such things as start more than one iteration simultaneously, or perform various operations while iterating through the collection using the iterator object, or even try to modify the collection while using the iterator to visit its elements.
This last idea might be a dangerous one. Namely, the iterator object (enumerator in .NET terms) keeps track of the current element and exposes the operation to move to the next element. Should we make changes to the underlying data structure, the data we have in the iterator might be incorrect. It could happen that the iterator picks wrong element as the next one, or even to break due to impossible references.
Imagine what would happen if we removed from the collection the element which is pointed by the iterator right now. If we called the MoveNext() method after that, which element should be the next? Such an operation is undefined for an element which is not in the collection, which means that perfectly valid sequence of calls to the MoveNext() method has brought the iterator into an impossible state. That should never happen.
To mitigate the issue, many implementations of the Iterator pattern assign version number or similar tag which identifies current state of the collection. Any method which changes the items stored in the collection internally changes the version. On the other hand, iterator object keeps record of the version which was in effect at the moment when it was created. Every call to iterator’s methods must check whether its version number matches the collection’s version number. Only if these two are equal shall the iterator proceed with the operation.
.NET Framework is no different in this respect. Internally, it uses a signed 32-bit integer number in its collections defined in the System.Collections and System.Collections.Generic namespaces. All methods that change contents of the collection increment this number by one before returning. That is .NET Framework’s way of making sure that the collection will not change while anyone is actively using the iterator extracted from it.
This can easily be demonstrated if we try to modify the collection while an iterator is used to traverse its elements, like in the following code segment.
using System;
using System.Collections.Generic;
namespace ConsoleDemo
{
class Program
{
static void Main(string[] args)
{
List<int> list = new List<int>();
list.AddRange(new int[] { 1, 2, 3, 4, 5 });
foreach (int value in list)
{
Console.Write("{0,3}", value);
// The next line will cause exception
// in the next iteration of the loop
// Cannot change collection while
// iterating through it
list[0] = 3;
}
Console.ReadLine();
}
}
}
When this piece of code is run, it results in an unhandled InvalidOperationException, thrown at the line where we are trying to set the first element of the list to value 3. This exception has occurred after the iterator, used internally by the foreach loop, has detected that the version of the list has advanced since the iterator was created.
On a related note, version counter wraps around once it reaches maximum positive integer value. This means that we could fool the list into belief that it wasn’t changed by setting the value of its element some four billion times:
using System;
using System.Collections.Generic;
namespace ConsoleDemo
{
class Program
{
static void Main(string[] args)
{
List<int> list = new List<int>();
list.AddRange(new int[] { 1, 2, 3, 4, 5 });
int pos = 0;
foreach (int value in list)
{
Console.Write("{0,3}", value);
// Repeating the change 2^32 times will
// fool the list to believe that nothing
// changed because version number will
// wrap around and come to the same value
for (Int64 i = 0; i < ((Int64)1) << 32; i++)
list[pos] = pos + 2;
pos++;
}
Console.WriteLine();
foreach (int value in list)
Console.Write("{0,3}", value);
Console.WriteLine();
Console.ReadLine();
}
}
}
This piece of code will work fine. It will print the list content twice on the console, and we will see that all members of the list have been effectively modified while iterating through it, without the iterator noticing that anything suspicious is happening. Here is the output produced by the application:
1 2 3 4 5
2 3 4 5 6
But this is just a funny piece of code and nothing else. For all practical purposes, 32-bit version number will do the job perfectly well in the List implementation. You may rest assured that continued use of the iterator after the collection content has changed will certainly cause the InvalidOperationException.
From this point on, we will align the terminology with .NET standards. Iterator will be named enumerator and it will implement IEnumerator interface. The object which produces the enumerator will be called collection.
The next point we will shed light on will tackle the issue of providing multiple concrete enumerator implementations for one concrete collection implementation. That is something IEnumerable interface does not provide out of the box, but sometimes becomes an important question when designing collections.
Supporting Multiple Iteration Algorithms
Sometimes, we want to leave the room open for different iteration algorithms. Classic textbook example is iterating through the binary tree. There we have preorder, inorder and postorder methods, each producing a different sequence of elements picked from the same tree.
The problem with this requirement is that the tree itself cannot implement IEnumerable interface. This is because IEnumerable only exposes one GetEnumerator() method, and that one without any arguments. It is impossible to tell, through means of IEnumerable interface, which iteration algorithm we desire. Therefore, this kind of declaration for the tree is impossible:
interface Tree<T> : IEnumerable<T>
{
}
To resolve the issue, we have to provide multiple GetEnumerator() methods, like here:
interface Tree<T>
{
IEnumerator<T> GetPrefixEnumerator();
IEnumerator<T> GetInfixEnumerator();
IEnumerator<T> GetPostfixEnumerator();
}
In this implementation, method name indicates the algorithm. It might be better if we could indicate the algorithm with an argument, but in that attempt we must think of tree’s encapsulation. Any iteration algorithm depends on internal organization of the tree data structure, which in turn jeopardizes its encapsulation. We will return to this problem later in this article.
Right now, we have reached one important conclusion. If the data structure implements IEnumerable interface directly, then it is doomed to only one iteration algorithm. This may be a needless constraint put up-front, even before concrete implementation comes. Implementing IEnumerable implies some default iteration sequence. But some concrete implementation might object to this, for example if general iteration is less optimal.
Implementing IEnumerable vs. Returning IEnumerable From a Method
Consider an abstract list as an example:
interface IList<T>: IEnumerable<T>
{
}
This looks fine, right? It looks right because we consider list a basic structure and we already have some ideas how we would use objects implementing the interface. Even without concrete list implementation, we can see code like this:
IList<int> data = ...
foreach (int value in data)
{
// ...
}
But what about the repository, for example:
interface IRepository<T> : IEnumerable<T>
{
}
Same thing, same implementation. But this doesn’t look right. The mere word “repository” carries stronger feelings than “list”. We consider repository an expensive object, the one which relies on storage, which always comes with performance penalty. In practice, repository is often declared like this:
interface IRepository<T>
{
IEnumerable<T> GetAll();
}
The trick with this declaration is that it lets us choose the iteration algorithm. There is this GetAll() method which suffers the full performance penalty, but the fact that it is not the only, mandatory method, means that we can add more of them:
interface IRepository<T>
{
IEnumerable<T> GetAll();
IEnumerable<T> Filter(Func<T, bool> predicate);
}
This flavor comes with the predicate that should be satisfied by elements returned from the repository. Concrete repositories could come up with internal optimization in presence of the predicate, who knows. Some implementations prefer LINQ expressions, rather than plain predicates:
interface IRepository<T>
{
IEnumerable<T> GetAll();
IEnumerable<T> Filter(Expression<Func<T, bool>> predicate);
}
Concrete implementations could then leverage expressions to exercise more optimized queries on the underlying storage. There is nothing wrong with this approach. It is a valid option when we have more or less clear picture of future concrete implementations that will need to incorporate filtering as part of the iterating algorithm.
Returning IEnumerable vs. Returning IEnumerator From a Method
Note that methods of the abstract repository given above are not returning IEnumerator. They return IEnumerable instead. That is another powerful concept. Not only that iteration algorithm has been externalized, but it has been represented as a separate view on the collection. It almost looks like the collection itself has been replicated to a separate object, which is then responsible to provide the enumerator on request.
But the collection did not replicate, of course. And that opens several questions, primarily regarding the question who is responsible to ensure that the collection does not change while enumerators are active on it.
On the other hand, returning IEnumerable from the method comes handy if you wish to use the foreach loop. This keyword actually expects IEnumerable, rather than IEnumerator. Therefore, returning IEnumerator from a method other than GetEnumerator() of the IEnumerable interface turns to be a bad idea. There is not much help from the language using such a method.
As an example, we can take a look at the array-like class which will support two iteration methods in the future: from front and from back. The basic implementation only supports adding elements:
class DynamicArray<T>
{
private T[] array;
private int count;
public DynamicArray()
{
this.array = new T[0];
}
public void Append(T value)
{
this.ResizeToFit(this.count + 1);
this.array[this.count] = value;
this.count++;
}
private void ResizeToFit(int desiredCount)
{
int newSize = this.array.Length;
while (newSize < desiredCount)
newSize = Math.Max(1, newSize * 2);
System.Array.Resize<T>(ref this.array, newSize);
}
}
Note that this class doesn’t implement the IEnumerable interface. I have a different plan. I will expose methods that return IEnumerable. Right now, it is only important to understand the basic flow of the dynamic array. It lets us append new elements freely and each time the internal array is completely filled up it gets resized so that more elements can be added. We can use this class in the following way:
DynamicArray<int> array = new DynamicArray<int>();
array.Append(3);
array.Append(2);
array.Append(5);
array.Append(1);
array.Append(4);
Anyway, we don’t have any methods of enumerating through the array’s content. If we wanted to expose a method which returns IEnumerator, that would not go that easy. We need a class implementing the IEnumerator interface:
class ArrayEnumerator<T> : IEnumerator<T>
{
private readonly T[] array;
private readonly int count;
private int pos;
public ArrayEnumerator(T[] array, int count)
{
this.array = array;
this.count = count;
this.pos = -1; // Invalid position
}
public T Current
{
get
{
if (this.pos < 0 || this.pos >= count)
throw new InvalidOperationException();
return this.array[this.pos];
}
}
public void Dispose()
{
}
object System.Collections.IEnumerator.Current
{
get
{
return this.Current;
}
}
public bool MoveNext()
{
this.pos++;
return this.pos < this.count;
}
public void Reset()
{
this.pos = -1;
}
}
Quite a lot of typing, you see. IEnumerator interface proposes members such as Current property getter, MoveNext() and Reset() methods. But that is not the only issue here. See how this enumerator receives the array and its used capacity through the constructor. This is the leaky abstraction. In order to work, this enumerator must know exact internal organization of the DynamicArray class.
But now that we have the enumerator class, we can use it in the DynamicArray quite easily:
class DynamicArray<T>
{
private T[] array;
private int count;
...
public IEnumerator<T> GetForwardEnumerator()
{
return new ArrayEnumerator<T>(this.array, this.count);
}
}
Then, things become more complicated at the using side again. With enumerators, C# syntax doesn’t help a bit:
DynamicArray<int> array = new DynamicArray<int>();
array.Append(3);
array.Append(2);
array.Append(5);
array.Append(1);
array.Append(4);
IEnumerator<int> enumerator = array.GetForwardEnumerator();
while (enumerator.MoveNext())
Console.Write("{0,3}", enumerator.Current);
Console.WriteLine();
This piece of code produces correct output:
3 2 5 1 4
But we had to rely on manual loop control, in form of the GetEnumerator-MoveNext-Current sequence of calls. This is not the preferable way.
It is much easier if we go with the method returning IEnumerable instead. For this occasion, C# comes with yield return/yield break keywords:
class DynamicArray<T>
{
private T[] array;
private int count;
...
public IEnumerable<T> GetForwardSequence()
{
for (int i = 0; i < this.count; i++)
yield return this.array[i];
}
}
And that is all! Only two lines of code effectively replace almost 50 lines of code we had to type to construct the enumerator class. Even more, this implementation is not leaky. DynamicArray is completely opaque, even with the GetForwardSequence() method in place. We are free to change internal organization, for example to use a List instead of the array, and nothing outside the DynamicArray will have to change. Further down the stream, client code becomes simpler as well, thanks to the foreach loop which works fine on the IEnumerable implementations:
DynamicArray<int> array = new DynamicArray<int>();
array.Append(3);
array.Append(2);
array.Append(5);
array.Append(1);
array.Append(4);
foreach (int value in array.GetForwardSequence())
Console.Write("{0,3}", value);
Console.WriteLine();
Infrastructure code is now gone. The client does not have to deal with enumerators at all.
Bottom line is that returning IEnumerator from the method costs us on more than one account:
- Implementation is much longer – We have to implement a new class implementing IEnumerator interface, which is far from trivial.
- Collection implementation leaks into the enumerator – Enumerator is dependent on concrete inner implementation of the collection. Should the collection change at some time, the enumerator implementation would also have to be modified. This is particularly painful if we have to maintain more than one enumerator in the system, where each enumerator implements one iteration algorithm.
- Client code is complicated – In order to traverse the collection, client has to deal with fairly complicated protocol imposed by the IEnumerator interface.
And, for the sake of completeness, let’s implement the back-to-front iterator for the dynamic array class:
class DynamicArray<T>
{
private T[] array;
private int count;
public DynamicArray()
{
this.array = new T[0];
}
public void Append(T value)
{
this.ResizeToFit(this.count + 1);
this.array[this.count] = value;
this.count++;
}
private void ResizeToFit(int desiredCount)
{
int newSize = this.array.Length;
while (newSize < desiredCount)
newSize = Math.Max(1, newSize * 2);
System.Array.Resize<T>(ref this.array, newSize);
}
public IEnumerable<T> GetForwardSequence()
{
for (int i = 0; i < this.count; i++)
yield return this.array[i];
}
public IEnumerable<T> GetBackwardSequence()
{
for (int i = this.count - 1; i >= 0; i--)
yield return this.array[i];
}
}
This is the complete source code of the dynamic array class. It exposes feature to append an element to the array, as well as to iterate through the array from the beginning or from the ending.
This implementation demonstrates the principle that the collection can benefit from avoiding to implement the IEnumerable interface. Instead, it can expose methods that return IEnumerable, letting the clients decide which iteration method they will request rather than establishing one iteration order as the default.
On the other hand, this code demonstrates how easy it is to write a method which returns IEnumerable using yield return/yield break instructions, though the technique gets more complicated as the underlying collection implementation grows more complex.
Custom Content Versioning Implementation
Now that we have a basic implementation of the dynamic array, we can think of more complicated scenarios. Suppose that we wanted to add a RemoveAt feature – a method which removes an element at specified position. Here is the code:
class DynamicArray<T>
{
private T[] array;
private int count;
public DynamicArray()
{
this.array = new T[0];
}
public void Append(T value)
{
this.ResizeToFit(this.count + 1);
this.array[this.count] = value;
this.count++;
}
public void RemoveAt(int pos)
{
if (pos < 0 || pos >= this.count)
throw new IndexOutOfRangeException();
for (int i = pos + 1; i < this.count; i++)
this.array[i - 1] = this.array[i];
this.count--;
this.Shrink();
}
private void ResizeToFit(int desiredCount)
{
int newSize = this.array.Length;
while (newSize < desiredCount)
newSize = Math.Max(1, newSize * 2);
System.Array.Resize<T>(ref this.array, newSize);
}
private void Shrink()
{
if (this.array.Length < this.count * 2)
return;
int newSize = this.array.Length;
while (newSize >= this.count * 2)
newSize = 2;
System.Array.Resize(ref this.array, newSize);
}
public IEnumerable<T> GetForwardSequence()
{
for (int i = 0; i < this.count; i++)
yield return this.array[i];
}
public IEnumerable<T> GetBackwardSequence()
{
for (int i = this.count - 1; i >= 0; i--)
yield return this.array[i];
}
}
This is the complete source code of the DynamicArray generic class. In addition to Append() method, now it contains the RemoveAt() method, which simply moves all subsequent elements by one position towards the beginning of the array and reduces the used size of the array. Quite simple feature, but it has introduced a defect to the design. Let’s see how it goes with enumerating the elements of the array and removing all visited elements at the same time:
DynamicArray<int> array = new DynamicArray<int>();
array.Append(3);
array.Append(2);
array.Append(5);
array.Append(1);
array.Append(4);
foreach (int value in array.GetForwardSequence())
{
Console.Write("{0,3}", value);
array.RemoveAt(0);
}
Console.WriteLine();
To be honest, it is hard to tell what this loop is supposed to print. Should it print the whole array, despite the fact that its content is being moved with each iteration? Whatever the intention, here is what the loop really prints out:
3 5 4
This is somewhere in between of whatever we could expect. The loop has printed some elements of the array, while at the same time skipping the others. Values 1 and 2 existed in the array but did not appear in the output. This is typical erratic behavior of structures that allow iteration but do not check whether the content has changed while some enumerator was active.
Long story short – we need to introduce versioning to the class. As soon as the enumerator desires to move through the collection, and its version doesn’t match the value it had when iteration started, the enumerator fails without further checking. It doesn’t matter whether the next step would be successful or would it cause an exception deep inside the class. Even if there is no exception, the operation could silently run incorrectly like we saw above, which is even worse option.
So, here is the implementation. We are introducing the version field in the DynamicArray class. Operations like Append() and RemoveAt() increment the version number. To avoid the historical problem of .NET collections, we are using 64-bit unsigned version numbers, which ensures that version will never repeat during the lifetime of an object. Here is the complete implementation of the DynamicArray class with custom version checking:
class DynamicArray<T>
{
private T[] array;
private int count;
private UInt64 version;
public DynamicArray()
{
this.array = new T[0];
}
public void Append(T value)
{
this.ResizeToFit(this.count + 1);
this.array[this.count] = value;
this.count++;
this.version++;
}
public void RemoveAt(int pos)
{
if (pos < 0 || pos >= this.count)
throw new IndexOutOfRangeException();
for (int i = pos + 1; i < this.count; i++)
this.array[i - 1] = this.array[i];
this.count--;
this.Shrink();
this.version++;
}
private void ResizeToFit(int desiredCount)
{
int newSize = this.array.Length;
while (newSize < desiredCount)
newSize = Math.Max(1, newSize * 2);
System.Array.Resize<T>(ref this.array, newSize);
}
private void Shrink()
{
if (this.array.Length < this.count * 2)
return;
int newSize = this.array.Length;
while (newSize >= this.count * 2)
newSize = 2;
System.Array.Resize(ref this.array, newSize);
}
public IEnumerable<T> GetForwardSequence()
{
UInt64 initialVersion = this.version;
for (int i = 0; i < this.count; i++)
{
if (this.version != initialVersion)
throw new InvalidOperationException("Array has changed.");
yield return this.array[i];
}
}
public IEnumerable<T> GetBackwardSequence()
{
UInt64 initialVersion = this.version;
for (int i = this.count - 1; i >= 0; i--)
{
if (this.version != initialVersion)
throw new InvalidOperationException("Array has changed.");
yield return this.array[i];
}
}
}
This is the final implementation of the DynamicArray class. This time it comes with internal version number, which is increased every time the content of the collection changes. Enumerators on their end take a snapshot of the version number and then check it against current version whenever they make a move that could cause erratic behavior. All holes are plugged, and all users who try to change the collection while there are active enumerators on it will be punished accordingly.
Custom Collection with Mutable Values
Suppose that we want to implement binary tree collection. The tree would consist of nodes, each node carrying an informative content, like this:
class BinaryNode<T>
{
public BinaryNode<T> LeftChild { get; set; }
public BinaryNode<T> RightChild { get; set; }
public T Content { get; set; }
}
This class is just a DTO, data transfer object. It does not provide any behavior. But nodes can be combined by a proper collection class to construct a binary tree structure. Below is the BinaryTree generic class which leverages the BinaryNode class to implement the binary tree data structure.
class BinaryTree<T>
{
private BinaryNode<T> RootNode { get; set; }
private BinaryNode<T> Current { get; set; }
public void SetRoot(T content)
{
this.RootNode =
new BinaryNode<T>()
{
Content = content
};
this.Current = this.RootNode;
}
public void SetLeftChild(T content)
{
if (this.Current == null)
throw new InvalidOperationException("No current node.");
this.Current.LeftChild =
new BinaryNode<T>()
{
Content = content
};
this.Current = this.Current.LeftChild;
}
public void SetRightChild(T content)
{
if (this.Current == null)
throw new InvalidOperationException("No current node.");
this.Current.RightChild =
new BinaryNode<T>()
{
Content = content
};
this.Current = this.Current.RightChild;
}
public void MoveToRoot()
{
this.Current = this.RootNode;
}
public void MoveLeft()
{
if (this.Current == null)
throw new InvalidOperationException("No current node.");
this.Current = this.Current.LeftChild;
}
public void MoveRight()
{
if (this.Current == null)
throw new InvalidOperationException("No current node.");
this.Current = this.Current.RightChild;
}
}
Please take your time to analyze this implementation. You will see that it works on the principle of the cursor. There is the Current property which refers to currently selected node. This lets us set left and right child nodes on any of the nodes in the tree, provided that we have previously navigated to that particular node using one of the Move methods – MoveToRoot(), MoveLeft() and MoveRight().
With this tree structure implementation, we can construct an arithmetic expression, for example, with code like this:
BinaryTree<string> expression = new BinaryTree<string>();
expression.SetRoot("+");
expression.SetLeftChild("1");
expression.MoveToRoot();
expression.SetRightChild("/");
expression.SetLeftChild("1");
expression.MoveToRoot();
expression.MoveRight();
expression.SetRightChild("x");
This cryptic code segment constructs an expression 1 + 1/x. Not much fun. It will be better if we had some means to iterate through the tree. Binary trees have three standard traversal orders: preorder, in which the node is traversed before its left and right subtrees; inorder, in which left subtree is traversed first, followed by the current node and right subtree; and postorder, in which left and right subtrees are traversed before the node that holds them.
We can easily write three methods that return IEnumerable, one for each of the traversal algorithms. However, note that this tree class is mutable. It allows us to change the tree content while enumerating nodes. Like before, we have to protect the client from dangers of traversing and modifying the collection simultaneously. The solution will be the same as before – we will add a 64-bit unsigned integer which will play the role of the version number. Methods that can change the structure – SetRoot(), SetLeftChild() and SetRightChild() – will have to increment the version number. Here is the modified binary tree class:
class BinaryTree<T>
{
private BinaryNode<T> RootNode { get; set; }
private BinaryNode<T> Current { get; set; }
private UInt64 version;
public void SetRoot(T content)
{
this.RootNode =
new BinaryNode<T>()
{
Content = content
};
this.Current = this.RootNode;
this.version++;
}
public void SetLeftChild(T content)
{
if (this.Current == null)
throw new InvalidOperationException("No current node.");
this.Current.LeftChild =
new BinaryNode<T>()
{
Content = content
};
this.Current = this.Current.LeftChild;
this.version++;
}
public void SetRightChild(T content)
{
if (this.Current == null)
throw new InvalidOperationException("No current node.");
this.Current.RightChild =
new BinaryNode<T>()
{
Content = content
};
this.Current = this.Current.RightChild;
this.version++;
}
public void MoveToRoot()
{
this.Current = this.RootNode;
}
public void MoveLeft()
{
if (this.Current == null)
throw new InvalidOperationException("No current node.");
this.Current = this.Current.LeftChild;
}
public void MoveRight()
{
if (this.Current == null)
throw new InvalidOperationException("No current node.");
this.Current = this.Current.RightChild;
}
}
As you can see, all Set methods are increasing the version number. On the other hand, Move methods do not increase the version number. This is because Move methods do not produce any change to the data structure. It changes the state of the object, but data structure remains the same. Since enumerators are only interested to know the links between tree nodes, and these links did not change, there is no reason to increase the version number from inside any of the Move methods.
With version number in place, we can start implementing the three enumeration strategies. Preorder first:
class BinaryTree<T>
{
private BinaryNode<T> RootNode { get; set; }
private BinaryNode<T> Current { get; set; }
private UInt64 version;
...
public IEnumerable<T> GetPreorderSequence()
{
UInt64 initialVersion = this.version;
Stack<BinaryNode<T>> stack = new Stack<BinaryNode<T>>();
if (this.RootNode != null)
stack.Push(this.RootNode);
while (stack.Count > 0)
{
this.AssertVersion(initialVersion);
BinaryNode<T> current = stack.Pop();
if (current.RightChild != null)
stack.Push(current.RightChild);
if (current.LeftChild != null)
stack.Push(current.LeftChild);
yield return current.Content;
}
}
private void AssertVersion(UInt64 expectedVersion)
{
if (this.version != expectedVersion)
throw new InvalidOperationException("Collection has changed.");
}
}
Traversal algorithm is not that simple, admittedly. It is based on passing the tree nodes through the stack, pushing each of the nodes to the output as soon as it leaves the stack and pushing its child nodes for further processing. This way of doing things will ensure that each node will appear in the output right before its left subtree and then its right subtree. That is precisely the definition of the preorder sequence.
Observe how we are asserting the collection version with every step of the loop. That is the mandatory step when working with mutable collection content. This time the assertion itself is moved to a utility method AssertVersion(), because the same feature will appear in the remaining two enumeration methods.
On to the next method – the one which returns inorder sequence:
class BinaryTree<T>
{
private BinaryNode<T> RootNode { get; set; }
private BinaryNode<T> Current { get; set; }
private UInt64 version;
...
public IEnumerable<T> GetInorderSequence()
{
UInt64 initialVersion = this.version;
Stack<BinaryNode<T>> stack = new Stack<BinaryNode<T>>();
Stack<bool> isLeftTraversed = new Stack<bool>();
if (this.RootNode != null)
{
stack.Push(this.RootNode);
isLeftTraversed.Push(false);
}
while (stack.Count > 0)
{
this.AssertVersion(initialVersion);
BinaryNode<T> current = stack.Peek();
bool isCurrentLeftTraversed = isLeftTraversed.Peek();
if (isCurrentLeftTraversed)
{
stack.Pop();
isLeftTraversed.Pop();
if (current.RightChild != null)
{
stack.Push(current.RightChild);
isLeftTraversed.Push(false);
}
yield return current.Content;
}
else
{
isLeftTraversed.Pop();
isLeftTraversed.Push(true);
if (current.LeftChild != null)
{
stack.Push(current.LeftChild);
isLeftTraversed.Push(false);
}
}
}
}
private void AssertVersion(UInt64 expectedVersion)
{
if (this.version != expectedVersion)
throw new InvalidOperationException("Collection has changed.");
}
}
This time we are using stack to keep track of the nodes that we are traversing. In addition to the node itself, we have to keep track of an additional flag, indicating whether the left subtree has already been traversed or not. This is important, because in inorder sequence the node must wait until its left tree has been fully processed.
You can study this algorithm in detail if you like. We will swiftly move to the last enumeration algorithm, postorder:
class BinaryTree<T>
{
private BinaryNode<T> RootNode { get; set; }
private BinaryNode<T> Current { get; set; }
private UInt64 version;
...
public IEnumerable<T> GetPostorderSequence()
{
UInt64 initialVersion = this.version;
Stack<BinaryNode<T>> stack = new Stack<BinaryNode<T>>();
Stack<bool> areChildrenTraversed = new Stack<bool>();
if (this.RootNode != null)
{
stack.Push(this.RootNode);
areChildrenTraversed.Push(false);
}
while (stack.Count > 0)
{
this.AssertVersion(initialVersion);
BinaryNode<T> current = stack.Peek();
bool areCurrentChildrenTraversed = areChildrenTraversed.Peek();
if (areCurrentChildrenTraversed)
{
stack.Pop();
areChildrenTraversed.Pop();
yield return current.Content;
}
else
{
areChildrenTraversed.Pop();
areChildrenTraversed.Push(true);
if (current.RightChild != null)
{
stack.Push(current.RightChild);
areChildrenTraversed.Push(false);
}
if (current.LeftChild != null)
{
stack.Push(current.LeftChild);
areChildrenTraversed.Push(false);
}
}
}
}
private void AssertVersion(UInt64 expectedVersion)
{
if (this.version != expectedVersion)
throw new InvalidOperationException("Collection has changed.");
}
}
The postorder algorithm also relies on the stack structure, this time forcing the node to wait on the stack until both left and right subtree have been fully traversed. Only after that, the node will be pushed to the output. Note once again that every iteration of the loop begins with the call to AssertVersion() method. This ensures that the caller will receive an InvalidOperationException as soon as it tries to modify the tree while an enumerator is still active on the same tree.
We can demonstrate the use of this binary tree and all three of its iteration algorithms:
static void PrintSequence<T>(string label, IEnumerable<T> sequence)
{
Console.Write(label);
foreach (T value in sequence)
Console.Write(value);
Console.WriteLine();
}
static void Demo()
{
BinaryTree<string> expression = new BinaryTree<string>();
expression.SetRoot("+");
expression.SetLeftChild("1");
expression.MoveToRoot();
expression.SetRightChild("/");
expression.SetLeftChild("1");
expression.MoveToRoot();
expression.MoveRight();
expression.SetRightChild("x");
PrintSequence(" preorder: ", expression.GetPreorderSequence());
PrintSequence(" inorder: ", expression.GetInorderSequence());
PrintSequence("postorder: ", expression.GetPostorderSequence());
Console.ReadLine();
}
When this code is run, it produces correct output:
preorder: +1/1x
inorder: 1+1/x
postorder: 11x/+
This concludes implementation of all three iteration algorithms on the binary tree data structure which allows us to change its contained nodes. Lesson learned from this exercise is that we must track content version all the time. The root cause of this requirement is that content of the collection is mutable. Not only that BinaryNode class is mutable, but BinaryTree class is actually mutating the node objects from its Set methods. That promises troubles when it comes to enumerating tree nodes, and consequently we have to track content version.
On a related note, BinaryTree class has turned to be quite long and complicated. This will give rise to a different idea – to externalize enumeration algorithm. We already had this idea before and now we are close to returning to it. If we could move preorder, inorder and postorder algorithms to separate classes, then the BinaryTree class would be reduced to a half of its current size in terms of number of lines of code. But that is not all. With proper enumeration classes, we could even produce more elegant code than the one demonstrated in the BinaryTree class.
But let’s not hurry ahead. There is one more idea that we should analyze before externalizing iteration algorithms. Namely, if tree nodes could be immutable, then there would be no way to change any actual tree representation that is currently being enumerated, even if the containing tree object has been changed. This may sound like a mind-bending idea, but it is actually very simple. That is precisely what we are going to do next.
Custom Collection with Immutable Nodes
One of the complications we had in the example with binary tree is that the tree structure can change while an enumerator is active on it. This could lead to improper behavior – sequence of tree elements that appear on the output could differ from both current and original content of the tree and actual sequence would be clearly incorrect.
We have already seen one method of dealing with the problem in previous section, where the tree class was maintaining the version number. This has solved the problem, but the solution has an unpleasant side-effect. Sometimes, the caller could receive an InvalidOperationException, if it has modified the tree structure while iterating it. Could we write such BinaryTree implementation which doesn’t throw exception if the caller has tried to modify it while iterating?
As a matter of fact, we could improve the situation by making BinaryNode objects immutable. Instead of modifying any node in the tree, we could replace it with completely new node. Here is the new implementation of the BinaryNode class:
class BinaryNode<T>
{
public T Content { get; private set; }
public BinaryNode<T> LeftChild { get; private set; }
public BinaryNode<T> RightChild { get; private set; }
public BinaryNode(T content): this(content, null, null)
{
}
private BinaryNode(T content, BinaryNode<T> leftChild, BinaryNode<T> rightChild)
{
this.Content = content;
this.LeftChild = leftChild;
this.RightChild = rightChild;
}
public BinaryNode<T> WithContent(T content)
{
return new BinaryNode<T>(content, this.LeftChild, this.RightChild);
}
public BinaryNode<T> WithLeftChild(BinaryNode<T> leftChild)
{
return new BinaryNode<T>(this.Content, leftChild, this.RightChild);
}
public BinaryNode<T> WithRightChild(BinaryNode<T> rightChild)
{
return new BinaryNode<T>(this.Content, this.LeftChild, rightChild);
}
}
This is the immutable binary node. It carries data and holds references to left and right subtrees. But it doesn’t let us change any of these. Should we want to change the node, we would have to construct a new one.
Note also that the only public constructor is the one which only receives the data content. Child references will be constructed through the use of WithLeftChild() and WithRightChild() methods, which will enforce a well-defined process of constructing the binary tree one step at the time. Also, there is this SetContent() method which produces a new node with same child references, but modified content.
Now comes the BinaryTree. It will start with still holding references to the root and current node, but this time adding a child will be a more elaborate operation.
class BinaryTree<T>
{
private BinaryNode<T> RootNode { get; set; }
private BinaryNode<T> Current { get; set; }
public void SetLeftChild(T content)
{
if (this.Current == null)
throw new InvalidOperationException("No current node.");
BinaryNode<T> childNode = new BinaryNode<T>(content);
this.Current = childNode;
// But... what now?
}
}
Here is the first attempt. And immediately we get stuck. The SetLeftChild() method is now in trouble. It has no way to attach the new node to the left of the Current node. The only way to do that is to recreate the Current node with new left child. But then we have a different sort of trouble. Current node is also a child (left or right) of somebody else. If we recreate Current, then its own parent will have to be modified to point to the new child. The story goes recursively on all the way until root node is hit.
This discussion shows all the ups and downs of the collection with immutable nodes. All the objects we modify remain intact, though they have to be effectively removed from the structure. All their new versions are constructed as new objects and inserted into the structure. This may cause a shockwave of changes through the whole data structure. But the overall result is that both old and new version of the data structure remain valid at the same time. The old tree and the new tree continue to live in memory side by side as long as there is at least one reference to them.
New tree will continue to live in memory thanks to the RootNode reference which keeps it alive and out of reach of the garbage collector. Old tree will continue to live as long as there is any enumerator holding a reference to it. That is the value returned from immutable nodes. Price we had to pay to reach this design is time required to restructure the tree when the node is changed.
Whether the price is worth the benefit is determined by the depth of the tree. If tree is more-or-less well balanced, the price could below. In perfectly balanced tree with N nodes, changing any node would take no more than log2(N) steps. In totally unbalanced tree, with depth of the tree equal to the number of nodes N it contains, changing one node would in the worst case require N nodes to change.
This could be unacceptable in practical cases, thought that is not certain either. We could go fine with O(N) cost on tree update if we know that the tree will be small and updates will be rare. When working with designs like this one, be sure to know the context in which the implementation will be running before applying it.
If we suppose that the cost of changing the tree is acceptable, we can continue with implementation. In order to modify all parents up the tree, we need the way to update the parent node from any other node. The node could hold a reference to parent node, but that would not be enough. We also have to know whether it is left or right child to its parent in order to perform the operation.
Code is telling more than words. Below is the complete implementation of the BinaryTree class, including the three GetSequence() methods. Implementation is admittedly complicated. The complexity comes with the requirement that contained nodes should be immutable. Take your time to study the implementation and then step forward to the discussion that follows.
class BinaryTree<T>
{
private BinaryNode<T> RootNode { get; set; }
private Stack<BinaryNode<T>> Path { get; set; }
private Stack<Func<BinaryNode<T>, BinaryNode<T>, BinaryNode<T>>>
TransformFunction { get; set; }
private BinaryNode<T> Current
{
get
{
if (this.Path.Count == 0)
throw new InvalidOperationException("No current node.");
return this.Path.Peek();
}
}
public BinaryTree()
{
this.Path = new Stack<BinaryNode<T>>();
this.TransformFunction =
new Stack<Func<BinaryNode<T>, BinaryNode<T>, BinaryNode<T>>>();
}
public void SetRoot(T content)
{
this.Path.Clear();
this.TransformFunction.Clear();
this.RootNode = new BinaryNode<T>(content);
this.Path.Push(this.RootNode);
}
public void SetLeftChild(T content)
{
BinaryNode<T> childNode = new BinaryNode<T>(content);
TransformFunction.Push((parent, child) => parent.WithLeftChild(child));
this.Path.Push(childNode);
this.RestructurePath();
}
public void SetRightChild(T content)
{
BinaryNode<T> childNode = new BinaryNode<T>(content);
TransformFunction.Push((parent, child) => parent.WithRightChild(child));
this.Path.Push(childNode);
this.RestructurePath();
}
public void SetContent(T content)
{
BinaryNode<T> newNode = this.Current.WithContent(content);
this.Path.Pop();
this.Path.Push(newNode);
this.RestructurePath();
}
private void RestructurePath()
{
Stack<BinaryNode<T>> restructuredNodes = new Stack<BinaryNode<T>>();
Stack<Func<BinaryNode<T>, BinaryNode<T>, BinaryNode<T>>> restructuredTransforms =
new Stack<Func<BinaryNode<T>, BinaryNode<T>, BinaryNode<T>>>();
BinaryNode<T> nextChild = this.Path.Pop();
restructuredNodes.Push(nextChild);
while (this.Path.Count > 0)
{
Func<BinaryNode<T>, BinaryNode<T>, BinaryNode<T>> transform =
this.TransformFunction.Pop();
BinaryNode<T> node = this.Path.Pop();
BinaryNode<T> restructuredNode = transform(node, restructuredNodes.Peek());
restructuredNodes.Push(restructuredNode);
restructuredTransforms.Push(transform);
}
this.RootNode = restructuredNodes.Peek();
while (restructuredNodes.Count > 0)
{
this.Path.Push(restructuredNodes.Pop());
}
while (restructuredTransforms.Count > 0)
{
this.TransformFunction.Push(restructuredTransforms.Pop());
}
}
public void MoveToRoot()
{
while (this.Path.Count > 1)
{
this.Path.Pop();
this.TransformFunction.Pop();
}
}
public void MoveLeft()
{
if (this.Current.LeftChild == null)
throw new InvalidOperationException("No left child.");
this.TransformFunction.Push((parent, child) => parent.WithLeftChild(child));
this.Path.Push(this.Current.LeftChild);
}
public void MoveRight()
{
if (this.Current.RightChild == null)
throw new InvalidOperationException("No right child.");
this.TransformFunction.Push((parent, child) => parent.WithRightChild(child));
this.Path.Push(this.Current.RightChild);
}
public IEnumerable<T> GetPreorderSequence()
{
Stack<BinaryNode<T>> stack = new Stack<BinaryNode<T>>();
if (this.RootNode != null)
stack.Push(this.RootNode);
while (stack.Count > 0)
{
BinaryNode<T> current = stack.Pop();
if (current.RightChild != null)
stack.Push(current.RightChild);
if (current.LeftChild != null)
stack.Push(current.LeftChild);
yield return current.Content;
}
}
public IEnumerable<T> GetInorderSequence()
{
Stack<BinaryNode<T>> stack = new Stack<BinaryNode<T>>();
Stack<bool> isLeftTraversed = new Stack<bool>();
if (this.RootNode != null)
{
stack.Push(this.RootNode);
isLeftTraversed.Push(false);
}
while (stack.Count > 0)
{
BinaryNode<T> current = stack.Peek();
bool isCurrentLeftTraversed = isLeftTraversed.Peek();
if (isCurrentLeftTraversed)
{
stack.Pop();
isLeftTraversed.Pop();
if (current.RightChild != null)
{
stack.Push(current.RightChild);
isLeftTraversed.Push(false);
}
yield return current.Content;
}
else
{
isLeftTraversed.Pop();
isLeftTraversed.Push(true);
if (current.LeftChild != null)
{
stack.Push(current.LeftChild);
isLeftTraversed.Push(false);
}
}
}
}
public IEnumerable<T> GetPostorderSequence()
{
Stack<BinaryNode<T>> stack = new Stack<BinaryNode<T>>();
Stack<bool> areChildrenTraversed = new Stack<bool>();
if (this.RootNode != null)
{
stack.Push(this.RootNode);
areChildrenTraversed.Push(false);
}
while (stack.Count > 0)
{
BinaryNode<T> current = stack.Peek();
bool areCurrentChildrenTraversed = areChildrenTraversed.Peek();
if (areCurrentChildrenTraversed)
{
stack.Pop();
areChildrenTraversed.Pop();
yield return current.Content;
}
else
{
areChildrenTraversed.Pop();
areChildrenTraversed.Push(true);
if (current.RightChild != null)
{
stack.Push(current.RightChild);
areChildrenTraversed.Push(false);
}
if (current.LeftChild != null)
{
stack.Push(current.LeftChild);
areChildrenTraversed.Push(false);
}
}
}
}
}
The first change in the design of this class is that now we are tracking the full path to the current node. Since we have to recreate the node and all its parents, this path will be the source of information how we got where we are. Next to this stack, there is the stack of transformation routines. In each step from a parent to a child node, we have to remember whether we went left or right. But instead of keeping the stack of left-right flags, which would cause quite a few if-then-else statements later, this implementation takes a different route. It keeps the stack of transformation routines, each routine receiving parent and (new) child objects and re-creates the parent to point to the new child.
The way we use this second stack of transformation routines becomes obvious from the SetLeftChild() and SetRightChild() methods. In both cases, we push a specific transformation function to this stack.
And then comes the most important part of the implementation – RestructurePath() method. This method pops all the elements from both stacks and applies transform functions to each of the nodes along the route. Once done, it pushes all the new elements back to the path stack, so that it looks like nothing has changed.
The code is complete. We can start the demonstration with simple example which tries the basic functionality:
BinaryTree<string> expression = new BinaryTree<string>();
expression.SetRoot("+");
expression.SetLeftChild("1");
expression.MoveToRoot();
expression.SetRightChild("/");
expression.SetLeftChild("1");
expression.MoveToRoot();
expression.MoveRight();
expression.SetRightChild("x");
PrintSequence(" preorder: ", expression.GetPreorderSequence());
PrintSequence(" inorder: ", expression.GetInorderSequence());
PrintSequence("postorder: ", expression.GetPostorderSequence());
This piece of code creates the tree representing the expression 1 + 1/x. When code is run, it prints this expression tree in preorder, inorder and postorder:
preorder: +1/1x
inorder: 1+1/x
postorder: 11x/+
This looks fine. Now a harder case – changing the tree while enumerating its elements:
BinaryTree<string> expression = new BinaryTree<string>();
expression.SetRoot("+");
expression.SetLeftChild("1");
expression.MoveToRoot();
expression.SetRightChild("/");
expression.SetLeftChild("1");
expression.MoveToRoot();
expression.MoveRight();
expression.SetRightChild("x");
foreach (string value in expression.GetInorderSequence())
{
Console.Write(value);
expression.MoveToRoot();
expression.MoveRight();
expression.MoveLeft();
expression.SetContent("2");
}
Console.WriteLine();
foreach (string value in expression.GetInorderSequence())
{
Console.Write(value);
}
Console.WriteLine();
In this example, the first loop iterates through the inorder representation of the expression tree and prints it out. But at the same time, the loop is changing the constant in the expression, so that the expression becomes 1 + 2/x. The trick with this example is that the loop is changing the part of the expression it still hasn’t reached. The second loop is there to walk through the expression once again and print it. Here is the output produced by this code:
1+1/x
1+2/x
As you can see, both loops are printing the expression as it looked when the loop started. Changing the tree while enumerator was active on it didn’t produce any effect on the current enumerator. But it has affected the next one, which still wasn’t created at that moment.
This feature comes for free when working with collections with immutable nodes. All enumerators are mutually independent and isolated from each other. It is possible to iterate the collection and prune it at the same time. It is possible to iterate the collection and modify its content at the same time.
There is one additional benefit that we have with this implementation. It never throws InvalidOperationException. Throwing this kind of exception is probably one of the worst decisions we are forced to make. When we throw InvalidOperationException, we admit that we have exposed a feature to the client, but at the same time we hope the client will not call it. That is a ridiculous situation. But very often, like in this case with enumerators, we cannot adapt the public interface of the class to the situation that the method is sometimes not available. Alternate design could be possible, though. In this section we have demonstrated that an enumerator which works on a collection containing immutable elements doesn’t have to throw InvalidOperationException. That should definitely be added to the list of positive effects of this kind of design.
But this great flexibility comes with the price. The price is added complexity, which is probably less important, but also a possible performance penalty, which could be of great importance in some cases. Hence, the decision must be made.
In the binary tree example we had an obvious performance penalty: changing an element of the tree requires a change in all nodes between it and the root, inclusive. In highly unbalanced trees, this could easily become equal to total number of nodes in the tree, which would then probably render the whole solution useless. If that happens, we must step back to a less powerful collection implementation, such as the tree with mutable nodes.
Lesson learned from this extensive example is that immutable nodes in the data structure offer great power over enumerators, but may impose performance penalty on the structure itself. Think twice before applying this technique.
Changing the Collection While Enumerating its Elements
Is there anyone in the C# community who didn’t try something similar to this:
List<int> list = new List<int>(new[] { 1, 2, 3, 4, 5 });
foreach (int value in list)
if (value % 2 == 0)
list.Remove(value);
This loop is supposed to remove even numbers from the list while iterating through it. It is a failure on two accounts. Not only that this approach is ineffective, because Remove() method takes O(N) time, taking the loop to complete only in O(N^2) time, but the whole attempt to modify the list while enumerating its elements is doomed. The list will throw InvalidOperationException as soon as MoveNext() method is invoked on the enumerator after changing the list.
We have already seen that this doesn’t have to be the case with all collections. If the collection is based on immutable data-carrying nodes, then this attempt wouldn’t have to look so foolish.
In the previous section we have seen a complete implementation of the binary tree structure which only contains immutable tree nodes. Whenever a change is made to a tree node, the node is replaced with the new one. In that way, any enumerator that might be active on the tree structure would still see the content it used to see when it was created. This almost looks like every new enumerator causes the collection to take a snapshot of its current state. Subsequent changes to its content would only affect subsequent enumerators, but not the snapshots that were served to previous enumerators.
But implementation from the previous section did not solve all the issues we might encounter in practice. If we really wanted to be able to change the collection while iterating through it, then every data node in the underlying data structure would have to be identified in a way which doesn’t change over time, even when the node object is recreated. That would give us the way to uniquely refer tree nodes without having actual access to them.
Code tells more than words. Below is the implementation of the BinaryNode class which supports node identity:
class BinaryNode<T>
{
public Guid Id { get; }
public T Content { get; }
public BinaryNode<T> LeftChild { get; }
public BinaryNode<T> RightChild { get; }
public BinaryNode(T content)
{
this.Content = content;
this.Id = Guid.NewGuid();
}
private BinaryNode(T content, BinaryNode<T> leftChild, BinaryNode<T> rightChild,
Guid id)
{
this.Content = content;
this.LeftChild = leftChild;
this.RightChild = rightChild;
this.Id = id;
}
public BinaryNode<T> WithContent(T content)
{
return new BinaryNode<T>(content, this.LeftChild, this.RightChild, this.Id);
}
public BinaryNode<T> WithLeftChild(BinaryNode<T> leftChild)
{
return new BinaryNode<T>(this.Content, leftChild, this.RightChild, this.Id);
}
public BinaryNode<T> WithRightChild(BinaryNode<T> rightChild)
{
return new BinaryNode<T>(this.Content, this.LeftChild, rightChild, this.Id);
}
public BinaryNode<T> WithRefreshedChild(BinaryNode<T> child)
{
BinaryNode<T> leftChild = this.LeftChild;
if (leftChild != null && child != null && leftChild.Id == child.Id)
leftChild = child;
BinaryNode<T> rightChild = this.RightChild;
if (rightChild != null && child != null && rightChild.Id == child.Id)
rightChild = child;
return new BinaryNode<T>(this.Content, leftChild, rightChild, this.Id);
}
public override string ToString()
{
return
this.LeftChild?.ToString() +
this.Content.ToString() +
this.RightChild?.ToString();
}
}
Primary change in this implementation is appearance of the Id property, which is initialized when the tree node is first created. All subsequent operations to the same node, operations that produce a modified copy of the node, will preserve the same Id value. This will let the tree track evolution of all its nodes.
On the other hand, if we wanted to manipulate the tree, we would have to know at least something about contained nodes. This means that the collection must allow implementation to leak to a certain degree. This is very important. In any design, if we want the client to manage the object, we have to give out some information about how the object is operating.
But we have to strike the right balance. The goal in this game of leaking the implementation is to only give out the necessary minimum of information. Any concept that becomes visible to the client immediately becomes client’s burden. It will be the client’s responsibility to deal with it properly from that point on. It will be the client’s responsibility to link to proper implementation. The client used to be the client of the binary tree, but now it becomes the client to an inner part of the binary tree. We should do everything in our power to reduce the amount of knowledge that will be required from the client to keep using its dependency.
For example, we could keep hiding the fact that the tree consists of BinaryNode objects, but we could not hide anymore that binary nodes are identified by a GUID. Methods that manipulate content of the tree will now return GUID which is assigned to the newly created node. That will let the client keep record of important nodes and then refer them back when modifying the tree.
But again that will not be enough. Sometimes, the client will desire to navigate the tree content while making changes. We will have to provide even more functionality for this purpose, but exposing the BinaryNode class itself would be way too much. BinaryNode is the essence of this implementation; it knows everything about inner organization of the tree. Giving that class in the hands of the client would make the client depend on details it doesn’t really need. For example, BinaryNode explains the way in which left or right child is set on the tree node. That is pure implementation detail and client should not depend on it.
To resolve the problem, we can expose a small wrapper around the BinaryNode and use it only as a cursor. It would let the client navigate around the tree, but not make changes. Here is the implementation of the NodeMetadata class which serves this precise purpose:
class NodeMetadata<T>
{
private BinaryNode<T> Node { get; }
private Func<BinaryNode<T>, bool> HasParentFunction { get; }
private Func<BinaryNode<T>, NodeMetadata<T>> GetParentFunction { get; }
public NodeMetadata(BinaryNode<T> node,
Func<BinaryNode<T>, bool> hasParent,
Func<BinaryNode<T>, NodeMetadata<T>> getParent)
{
if (node == null)
throw new ArgumentNullException(nameof(node));
this.Node = node;
this.HasParentFunction = hasParent;
this.GetParentFunction = getParent;
}
public T Content
{
get
{
return this.Node.Content;
}
}
public Guid Id
{
get
{
return this.Node.Id;
}
}
public bool HasLeftChild
{
get
{
return this.Node.LeftChild != null;
}
}
public NodeMetadata<T> LeftChild
{
get
{
return new NodeMetadata<T>(this.Node.LeftChild,
this.HasParentFunction,
this.GetParentFunction);
}
}
public bool HasRightChild
{
get
{
return this.Node.RightChild != null;
}
}
public NodeMetadata<T> RightChild
{
get
{
return new NodeMetadata<T>(this.Node.RightChild,
this.HasParentFunction,
this.GetParentFunction);
}
}
public bool HasParent
{
get
{
return this.HasParentFunction(this.Node);
}
}
public NodeMetadata<T> Parent
{
get
{
if (!this.HasParent)
throw new InvalidOperationException("There is no parent.");
return this.GetParentFunction(this.Node);
}
}
public bool IsLeftChild
{
get
{
if (!this.HasParent)
return false;
BinaryNode<T> leftChild = this.Parent.Node.LeftChild;
if (leftChild == null)
return false;
Guid leftChildId = leftChild.Id;
return this.Node.Id == leftChildId;
}
}
public override string ToString()
{
return this.Content.ToString();
}
}
This class only exposes queries. The client can ask the metadata object about the node containing certain data, including asking questions about nodes that exist above and below the node represented by the node managed by particular metadata object.
Observe the way navigation to parent node is implemented. Neither BinaryNode nor NodeMetadata can conclude which node is above the current one. For BinaryNode class that would be impossible to implement. Having both child and parent references creates circular references between objects. That is not the problem itself, but it becomes impossible to achieve with immutable objects. In order to construct an object graph with circles, some object must be created first and then modified later after objects it points to are constructed. With immutable objects this plan fails. Bottom line is that the immutable tree node can either point to its children or to its parent, not both. In this implementation I have decided to refer to child nodes because that makes insert operations much easier to manage. But that means that node cannot figure its parent without help from the outside.
And the same situation happens with the NodeMetadata class, which is just a wrapper around BinaryNode. Since node doesn’t know its parent, metadata object cannot tell it either. But I wanted to implement two-way navigation using metadata objects and for that reason NodeMetadata expects functions to be supplied from the outside which would resolve the parent node on demand. These functions will then be supplied by the BinaryTree class which has a perfectly clear picture about which node is parent to which other nodes.
This finally makes it ready to implement the mutable binary tree which supports multiple immutable versions of its content. Each enumerator created on this tree will operate on a snapshot of the tree content and the snapshot will never change during the lifetime of the enumerator. On the other hand, tree itself could change, but as already said that change will not be visible to enumerators that have already been created. In order to see the change, we would have to ask for a fresh enumerator.
Why is this concept important? There are cases in practice when we have to modify the data structure, typically to purge some of its elements, but we don’t know what changes will be made before we traverse the structure. For example, we might have to adapt the expression tree to printout by injecting parentheses in it. But in order to determine precise locations of the parentheses, we have to traverse the expression tree in order to identify operation nodes that have to be parenthesized.
Typical approach to this kind of problems is to construct another data structure while iterating the first one, so that the new structure reflects desired changes. Once done, the second data structure would become active instead of the old one. But this approach produces higher memory footprint and requires many new objects to be constructed. This may come with performance penalty, though. In some cases it is possible to use immutable inner nodes and then to modify the structure while traversing it.
In this section we will first complete the implementation of the BinaryTree class which uses the immutable BinaryNode objects, and then use it to implement expression tree which can be modified during traversal.
The new BinaryTree implementation will generally turn around the notion of node Id. It will contain dictionaries which map Id values to actual nodes, as well as parent-child pairs. The latter will be there to enrich nodes with this missing information – reference to parent. To cut the long story short, BinaryTree implementation will begin with this skeleton:
class BinaryTree<T>
{
private Guid RootNodeId { get; set; }
private Dictionary<Guid, BinaryNode<T>> IdToNode { get; }
private Dictionary<Guid, Guid> NodeIdToParentId { get; }
public bool IsEmpty { get; }
public Guid SetRoot(T content) { ... }
public Guid SetLeftChildOn(Guid nodeId, T content) { ... }
public Guid SetRightChildOn(Guid nodeId, T content) { ... }
public void SetContentOf(Guid nodeId, T content) { ... }
public Guid InsertLeftChildOn(Guid nodeId, T content, bool existingChildToLeft) { ... }
public Guid InsertRightChildOn(Guid nodeId, T content, bool existingChildToLeft) { ... }
public IEnumerable<T> GetPreorderSequence() { ... }
public IEnumerable<T> GetInorderSequence() { ... }
public IEnumerable<T> GetPostorderSequence() { ... }
public IEnumerable<NodeMetadata<T>> GetPreorderMetaSequence() { ... }
public IEnumerable<NodeMetadata<T>> GetInorderMetaSequence() { ... }
public IEnumerable<NodeMetadata<T>> GetPostorderMetaSequence() { ... }
}
Public interface of the BinaryTree class can be split into two groups of methods. One group consists of Set and Insert methods. They are all designed to add new child nodes to the tree. Insert methods are there to insert a child to the node and move its current child deeper down. The other group consists of GetSequence methods. These methods return preorder, inorder and postorder sequences of tree elements. Additional variants are there to return sequences of metadata. Should we decide to involve more with the tree while enumerating its nodes, methods that return metadata sequences are the best choice.
Finally, we can provide the full implementation of the BinaryTree class. It is far from simple, so please take your time to digest it.
class BinaryTree<T>
{
private Guid RootNodeId { get; set; }
private Dictionary<Guid, BinaryNode<T>> IdToNode { get; }
private Dictionary<Guid, Guid> NodeIdToParentId { get; }
public bool IsEmpty
{
get
{
return this.IdToNode.Count == 0;
}
}
private BinaryNode<T> RootNode
{
get
{
// Throws if tree is empty
return this.IdToNode[this.RootNodeId];
}
}
public BinaryTree()
{
this.IdToNode = new Dictionary<Guid, BinaryNode<T>>();
this.NodeIdToParentId = new Dictionary<Guid, Guid>();
}
public Guid SetRoot(T content)
{
this.IdToNode.Clear();
this.NodeIdToParentId.Clear();
BinaryNode<T> node = this.CreateNode(content);
this.RootNodeId = node.Id;
return node.Id;
}
public Guid SetLeftChildOn(Guid nodeId, T content)
{
return this.SetChildOn(nodeId, content,
(parent) => parent.LeftChild,
(parent, child) => parent.WithLeftChild(child));
}
public Guid SetRightChildOn(Guid nodeId, T content)
{
return this.SetChildOn(nodeId, content,
(parent) => parent.RightChild,
(parent, child) => parent.WithRightChild(child));
}
public void SetContentOf(Guid nodeId, T content)
{
BinaryNode<T> node = this.FindNode(nodeId);
BinaryNode<T> newNode = node.WithContent(content);
this.RebuildPathToRoot(newNode);
}
public Guid InsertLeftChildOn(Guid nodeId, T content, bool existingChildToLeft)
{
BinaryNode<T> parent = FindNode(nodeId);
return this.InsertChild(content, parent.LeftChild, existingChildToLeft,
(child) => parent.WithLeftChild(child));
}
public Guid InsertRightChildOn(Guid nodeId, T content, bool existingChildToLeft)
{
BinaryNode<T> parent = FindNode(nodeId);
BinaryNode<T> childToMove = parent.RightChild;
return this.InsertChild(content, childToMove, existingChildToLeft,
(child) => parent.WithRightChild(child));
}
private Guid SetChildOn(Guid nodeId, T content,
Func<BinaryNode<T>, BinaryNode<T>> childToRemoveFunction,
Func<BinaryNode<T>, BinaryNode<T>, BinaryNode<T>> withChildFunction)
{
BinaryNode<T> parent = this.FindNode(nodeId);
BinaryNode<T> childToRemove = childToRemoveFunction(parent);
BinaryNode<T> child = this.CreateNode(content);
BinaryNode<T> newParent = withChildFunction(parent, child);
this.WithRelation(newParent, child);
this.RebuildPathToRoot(newParent);
if (childToRemove != null)
this.RemoveSubtree(childToRemove);
return child.Id;
}
private void RemoveSubtree(BinaryNode<T> childToRemove)
{
Queue<BinaryNode<T>> queue = new Queue<BinaryNode<T>>();
queue.Enqueue(childToRemove);
while (queue.Count > 0)
{
BinaryNode<T> node = queue.Dequeue();
this.IdToNode.Remove(node.Id);
if (this.NodeIdToParentId.ContainsKey(node.Id))
this.NodeIdToParentId.Remove(node.Id);
if (node.LeftChild != null)
queue.Enqueue(node.LeftChild);
if (node.RightChild != null)
queue.Enqueue(node.RightChild);
}
}
private Guid InsertChild(T content, BinaryNode<T> childToMove,
bool existingChildToLeft,
Func<BinaryNode<T>, BinaryNode<T>> withChildFunction)
{
BinaryNode<T> child = new BinaryNode<T>(content);
if (existingChildToLeft)
child = child.WithLeftChild(childToMove);
else
child = child.WithRightChild(childToMove);
BinaryNode<T> newNode = withChildFunction(child);
this.WithRelation(child, childToMove);
this.WithRelation(newNode, child);
this.RebuildPathToRoot(newNode);
return child.Id;
}
private BinaryNode<T> FindNode(Guid id)
{
return this.IdToNode[id]; // May throw
}
private BinaryNode<T> CreateNode(T content)
{
BinaryNode<T> node = new BinaryNode<T>(content);
this.RegisterNode(node);
return node;
}
private void RegisterNode(BinaryNode<T> node)
{
this.IdToNode[node.Id] = node;
}
private void RebuildPathToRoot(BinaryNode<T> node)
{
BinaryNode<T> current = node;
while (true)
{
this.RegisterNode(current);
if (!this.HasParent(current))
break;
BinaryNode<T> parent = this.GetParent(current);
current = parent.WithRefreshedChild(current);
}
}
private void WithRelation(Guid parentId, Guid childId)
{
this.NodeIdToParentId[childId] = parentId;
}
private void WithRelation(BinaryNode<T> parent, BinaryNode<T> child)
{
this.WithRelation(parent.Id, child.Id);
}
private bool HasParent(Guid id)
{
return this.NodeIdToParentId.ContainsKey(id);
}
private bool HasParent(BinaryNode<T> node)
{
return this.HasParent(node.Id);
}
private BinaryNode<T> GetParent(Guid id)
{
Guid parentId = this.NodeIdToParentId[id];
return FindNode(parentId);
}
private BinaryNode<T> GetParent(BinaryNode<T> node)
{
return this.GetParent(node.Id);
}
private NodeMetadata<T> GetParentMetadata(BinaryNode<T> node)
{
BinaryNode<T> parent = this.GetParent(node);
return this.MetadataFor(parent);
}
public IEnumerable<T> GetPreorderSequence()
{
return GetSequence(this.GetPreorderMetaSequence);
}
public IEnumerable<T> GetInorderSequence()
{
return GetSequence(this.GetInorderMetaSequence);
}
public IEnumerable<T> GetPostorderSequence()
{
return GetSequence(this.GetPostorderMetaSequence);
}
public IEnumerable<NodeMetadata<T>> GetPreorderMetaSequence()
{
Stack<BinaryNode<T>> stack = new Stack<BinaryNode<T>>();
if (!this.IsEmpty)
stack.Push(this.RootNode);
while (stack.Count > 0)
{
BinaryNode<T> current = stack.Pop();
if (current.RightChild != null)
stack.Push(current.RightChild);
if (current.LeftChild != null)
stack.Push(current.LeftChild);
yield return this.MetadataFor(current);
}
}
public IEnumerable<NodeMetadata<T>> GetInorderMetaSequence()
{
Stack<BinaryNode<T>> stack = new Stack<BinaryNode<T>>();
Stack<bool> isLeftTraversed = new Stack<bool>();
if (!this.IsEmpty)
{
stack.Push(this.RootNode);
isLeftTraversed.Push(false);
}
while (stack.Count > 0)
{
BinaryNode<T> current = stack.Peek();
bool isCurrentLeftTraversed = isLeftTraversed.Peek();
if (isCurrentLeftTraversed)
{
stack.Pop();
isLeftTraversed.Pop();
if (current.RightChild != null)
{
stack.Push(current.RightChild);
isLeftTraversed.Push(false);
}
yield return this.MetadataFor(current);
}
else
{
isLeftTraversed.Pop();
isLeftTraversed.Push(true);
if (current.LeftChild != null)
{
stack.Push(current.LeftChild);
isLeftTraversed.Push(false);
}
}
}
}
public IEnumerable<NodeMetadata<T>> GetPostorderMetaSequence()
{
Stack<BinaryNode<T>> stack = new Stack<BinaryNode<T>>();
Stack<bool> areChildrenTraversed = new Stack<bool>();
if (!this.IsEmpty)
{
stack.Push(this.RootNode);
areChildrenTraversed.Push(false);
}
while (stack.Count > 0)
{
BinaryNode<T> current = stack.Peek();
bool areCurrentChildrenTraversed = areChildrenTraversed.Peek();
if (areCurrentChildrenTraversed)
{
stack.Pop();
areChildrenTraversed.Pop();
yield return this.MetadataFor(current);
}
else
{
areChildrenTraversed.Pop();
areChildrenTraversed.Push(true);
if (current.RightChild != null)
{
stack.Push(current.RightChild);
areChildrenTraversed.Push(false);
}
if (current.LeftChild != null)
{
stack.Push(current.LeftChild);
areChildrenTraversed.Push(false);
}
}
}
}
private IEnumerable<T> GetSequence(Func<IEnumerable<NodeMetadata<T>>> metaSequenceGenerator)
{
foreach (NodeMetadata<T> node in metaSequenceGenerator())
yield return node.Content;
}
private NodeMetadata<T> MetadataFor(BinaryNode<T> node)
{
return new NodeMetadata<T>(node,
(child) => this.HasParent(child),
(child) => this.GetParentMetadata(child));
}
public override string ToString()
{
if (this.IsEmpty)
return string.Empty;
return this.RootNode.ToString();
}
}
What can we do with this class? We can, for example, build an expression tree, such as the one shown in the picture.
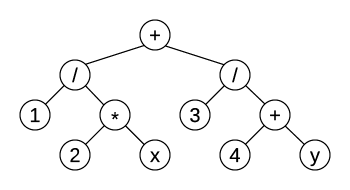
And here is the code which constructs this expression tree:
static void PrintSequence<T>(string label, IEnumerable<T> sequence)
{
Console.Write(label);
foreach (T value in sequence)
Console.Write(value);
Console.WriteLine();
}
static void Demo()
{
BinaryTree<string> expression = new BinaryTree<string>();
Guid plusId = expression.SetRoot("+");
Guid leftDivisionId = expression.SetLeftChildOn(plusId, "/");
expression.SetLeftChildOn(leftDivisionId, "1");
Guid multiplyId = expression.SetRightChildOn(leftDivisionId, "*");
expression.SetLeftChildOn(multiplyId, "2");
expression.SetRightChildOn(multiplyId, "x");
Guid divisionId = expression.SetRightChildOn(plusId, "/");
expression.SetLeftChildOn(divisionId, "3");
Guid denominatorPlusId = expression.SetRightChildOn(divisionId, "+");
expression.SetLeftChildOn(denominatorPlusId, "4");
expression.SetRightChildOn(denominatorPlusId, "y");
PrintSequence("expression: ", expression.GetInorderSequence());
}
In the Demo method we are carefully constructing the expression tree. We are remembering important node Ids as we progress. These Id values will then be passed to subsequent calls to add child nodes. When this method is run, it produces output like this:
expression: 1/2*x+3/4+y
This output is the inorder sequence of expression’s elements. But it is not printed right. Subexpressions 2*x and 4+y should take precedence over their neighboring operations. Without parentheses, this expression would read like (1/2)*x+(3/4)+y, although expression tree from which this printout has arrived clearly describes expression 1/(2*x)+3/(4+y).
We want to improve the printout capabilities of our expression trees and for that purpose we will provide an extension method named AddParentheses, which will be defined on a special case of BinaryTree<string>:
static class ExpressionTreeExtensions
{
public static void AddParentheses(this BinaryTree<string> tree)
{
foreach (NodeMetadata<string> node in tree.GetPreorderMetaSequence())
{
if (ShouldParenthesise(node))
{
// Chaning the structure while enumerating it!
tree.InsertLeftChildOn(node.Id, "(", false);
tree.InsertRightChildOn(node.Id, ")", true);
}
}
}
...
}
If you closely observe the implementation, you will see that AddParentheses() method is effectively changing the BinaryTree object while traversing it. That is something that would normally be prohibited. But thanks to the way in which BinaryTree class is implemented, this loop will actually work fine. Current enumerator, that which supplies values for the node variable, will not be able to see modifications made to the tree. But any iterator that comes later will observe the change.
On a semantic level, AddParentheses() method inserts opening and closing parentheses under the operation node which is of lower precedence than its parent. Additional criterion, as you can see from the complete listing of the ExpressionTreeExtensions class below, will be that parentheses are added if operator is of the same precedence as its parent operator, but it comes to the right. This is because all four arithmetic operators supported in this example are left-associative. Nevertheless, when AddParentheses() method is applied to the expression tree we had before, it adds parentheses like shown in the following picture:
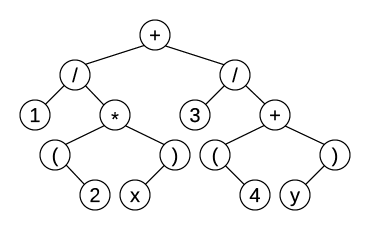
Now that we have AddParentheses() method implemented, we could extend the demonstration by calling the AddParentheses() method on the expression tree and then printing the expression again:
static void Demo()
{
...
PrintSequence("before: ", expression.GetInorderSequence());
expression.AddParentheses();
PrintSequence(" after: ", expression.GetInorderSequence());
}
This modified Demo() function prints both incorrect and correct expression:
before: 1/2*x+3/4+y
after: 1/(2*x)+3/(4+y)
As you can see, parentheses have been put right where they were supposed in the second expression. For the sake of completeness, below is the whole static class which holds the AddParentheses() extension method. Once again, the implementation is not simple. But it looks like nothing gets done in a simple way when it comes to binary trees.
static class ExpressionTreeExtensions
{
private readonly static string[] Operators =
new string[] { "+", "-", "*", "/" };
private readonly static string[] AdditiveOperators =
new string[] { "+", "-" };
public static void AddParentheses(this BinaryTree<string> tree)
{
foreach (NodeMetadata<string> node in tree.GetPreorderMetaSequence())
{
if (ShouldParenthesise(node))
{
// Chaning the structure while enumerating it!
tree.InsertLeftChildOn(node.Id, "(", false);
tree.InsertRightChildOn(node.Id, ")", true);
}
}
}
private static int GetOperatorPrecedence(string value)
{
if (!IsOperator(value))
return 0;
if (IsAdditiveOperator(value))
return 1;
return 2;
}
private static bool IsOperator(string value)
{
return Operators.Contains(value);
}
private static bool IsAdditiveOperator(string value)
{
return AdditiveOperators.Contains(value);
}
private static int ComparePrecendence(string oper1, string oper2)
{
int precedence = GetOperatorPrecedence(oper1);
int prevPrecendece = GetOperatorPrecedence(oper2);
return precedence.CompareTo(prevPrecendece);
}
private static int ComparePrecedenceWithParent(NodeMetadata<string> node)
{
if (!node.HasParent)
return 1;
string content = node.Content;
string parentContent = node.Parent.Content;
return ComparePrecendence(content, parentContent);
}
private static bool ShouldParenthesise(NodeMetadata<string> node)
{
if (!IsOperator(node.Content))
return false;
int precedence = ComparePrecedenceWithParent(node);
if (precedence < 0)
return true;
// Operators are left-associative
if (precedence == 0 && !node.IsLeftChild)
return true;
return false;
}
}
Lesson learned from this extensive example is that it is indeed possible to modify the collection while iterating through it. The operation comes with performance penalty, though. So in any practical case it would be necessary to measure this performance hit against the hit we have to sustain when modifying the collection by copying it on the side. Sometimes the former option will be the better suited one, sometimes the latter.
Externalizing the Enumeration Algorithm
By this point we were implementing iteration algorithms inside the container class. But that is not the best choice when there are multiple iteration algorithm, like with binary trees. Binary tree came with three iteration methods, each coming in two flavors – returning metadata or just returning data contained in nodes:
class BinaryTree<T>
{
...
public IEnumerable<T> GetPreorderSequence()
{
return GetSequence(this.GetPreorderMetaSequence);
}
public IEnumerable<T> GetInorderSequence()
{
return GetSequence(this.GetInorderMetaSequence);
}
public IEnumerable<T> GetPostorderSequence()
{
return GetSequence(this.GetPostorderMetaSequence);
}
public IEnumerable<NodeMetadata<T>> GetPreorderMetaSequence()
{
Stack<BinaryNode<T>> stack = new Stack<BinaryNode<T>>();
if (!this.IsEmpty)
stack.Push(this.RootNode);
while (stack.Count > 0)
{
BinaryNode<T> current = stack.Pop();
if (current.RightChild != null)
stack.Push(current.RightChild);
if (current.LeftChild != null)
stack.Push(current.LeftChild);
yield return this.MetadataFor(current);
}
}
public IEnumerable<NodeMetadata<T>> GetInorderMetaSequence()
{
Stack<BinaryNode<T>> stack = new Stack<BinaryNode<T>>();
Stack<bool> isLeftTraversed = new Stack<bool>();
if (!this.IsEmpty)
{
stack.Push(this.RootNode);
isLeftTraversed.Push(false);
}
while (stack.Count > 0)
{
BinaryNode<T> current = stack.Peek();
bool isCurrentLeftTraversed = isLeftTraversed.Peek();
if (isCurrentLeftTraversed)
{
stack.Pop();
isLeftTraversed.Pop();
if (current.RightChild != null)
{
stack.Push(current.RightChild);
isLeftTraversed.Push(false);
}
yield return this.MetadataFor(current);
}
else
{
isLeftTraversed.Pop();
isLeftTraversed.Push(true);
if (current.LeftChild != null)
{
stack.Push(current.LeftChild);
isLeftTraversed.Push(false);
}
}
}
}
public IEnumerable<NodeMetadata<T>> GetPostorderMetaSequence()
{
Stack<BinaryNode<T>> stack = new Stack<BinaryNode<T>>();
Stack<bool> areChildrenTraversed = new Stack<bool>();
if (!this.IsEmpty)
{
stack.Push(this.RootNode);
areChildrenTraversed.Push(false);
}
while (stack.Count > 0)
{
BinaryNode<T> current = stack.Peek();
bool areCurrentChildrenTraversed = areChildrenTraversed.Peek();
if (areCurrentChildrenTraversed)
{
stack.Pop();
areChildrenTraversed.Pop();
yield return this.MetadataFor(current);
}
else
{
areChildrenTraversed.Pop();
areChildrenTraversed.Push(true);
if (current.RightChild != null)
{
stack.Push(current.RightChild);
areChildrenTraversed.Push(false);
}
if (current.LeftChild != null)
{
stack.Push(current.LeftChild);
areChildrenTraversed.Push(false);
}
}
}
}
private IEnumerable<T> GetSequence(Func<IEnumerable<NodeMetadata<T>>> metaSequenceGenerator)
{
foreach (NodeMetadata<T> node in metaSequenceGenerator())
yield return node.Content;
}
private NodeMetadata<T> MetadataFor(BinaryNode<T> node)
{
return new NodeMetadata<T>(node,
(child) => this.HasParent(child),
(child) => this.GetParentMetadata(child));
}
}
Quite a lot of code for one class, especially when we know that these three methods are not related to each other. Could we move them out to separate classes? Well, obviously yes. But that comes with the twist.
If we wanted to move iteration algorithms to separate classes, then we had to tell out something about collection’s internal structure. We have to leak the implementation out of the collection, so that the enumerator can access its content. That is the price we pay for the comfort of reducing the collection class.
Below is the complete preorder enumerator class for the binary tree. It actually enumerates node metadata, which is constructed using the function provided by the tree. If you remember from the previous section, node metadata are more convenient for consumers because they allow navigation both upwards and downwards from any tree node. But on the flip side, the tree itself is the only object which knows how to map binary node to its metadata. Hence the mandatory argument in the constructor below which accepts factory method to produce metadata from a node.
class PreorderMetaEnumrator<T> : IEnumerator<NodeMetadata<T>>
{
private BinaryNode<T> RootNode { get; }
private Func<BinaryNode<T>, NodeMetadata<T>> NodeToMetadata { get; }
private Stack<BinaryNode<T>> UnprocessedNodes { get; }
private BinaryNode<T> CurrentNode { get; set; }
public PreorderMetaEnumrator(BinaryNode<T> rootNode,
Func<BinaryNode<T>, NodeMetadata<T>> nodeToMetadata)
{
this.RootNode = rootNode;
this.NodeToMetadata = nodeToMetadata;
this.UnprocessedNodes = new Stack<BinaryNode<T>>();
PushIfExists(rootNode);
}
public NodeMetadata<T> Current
{
get
{
if (this.CurrentNode == null)
throw new InvalidOperationException();
return this.NodeToMetadata(this.CurrentNode);
}
}
object IEnumerator.Current
{
get
{
return this.Current;
}
}
public void Dispose()
{
}
public bool MoveNext()
{
if (this.UnprocessedNodes.Count == 0)
{
this.CurrentNode = null;
return false;
}
this.CurrentNode = this.UnprocessedNodes.Pop();
this.PushIfExists(this.CurrentNode.RightChild);
this.PushIfExists(this.CurrentNode.LeftChild);
return true;
}
public void Reset()
{
this.CurrentNode = null;
this.UnprocessedNodes.Clear();
this.PushIfExists(this.RootNode);
}
private void PushIfExists(BinaryNode<T> node)
{
if (node == null)
return;
this.UnprocessedNodes.Push(node);
}
}
This is the whole implementation of the proper preorder enumerator for the binary tree. All this code used to reside in the binary tree class. And now it’s out, making the BinaryTree class somewhat shorter:
class BinaryTree<T>
{
...
public IEnumerable<T> GetPreorderSequence()
{
return this.GetSequence(this.GetPreorderMetaEnumerator());
}
public IEnumerable<NodeMetadata<T>> GetPreorderMetaSequence()
{
return this.GetMetaSequence(this.GetPreorderMetaEnumerator());
}
private IEnumerator<NodeMetadata<T>> GetPreorderMetaEnumerator()
{
return new PreorderMetaEnumrator<T>(this.RootNode, this.MetadataFor);
}
private IEnumerable<NodeMetadata<T>> GetMetaSequence(IEnumerator<NodeMetadata<T>> metaEnumerator)
{
while (metaEnumerator.MoveNext())
yield return metaEnumerator.Current;
}
private IEnumerable<T> GetSequence(IEnumerator<NodeMetadata<T>> metaEnumerator)
{
foreach (NodeMetadata<T> metadata in this.GetMetaSequence(metaEnumerator))
yield return metadata.Content;
}
private NodeMetadata<T> MetadataFor(BinaryNode<T> node)
{
return new NodeMetadata<T>(node,
(child) => this.HasParent(child),
(child) => this.GetParentMetadata(child));
}
...
}
This is all it takes to implement two methods that expose preorder sequence of nodes from the binary tree. Implementation on the collection side is quite effective and very short. We can provide two more enumerators which would cover inorder and postorder then. Inorder first:
class InorderMetaEnumerator<T> : IEnumerator<NodeMetadata<T>>
{
private BinaryNode<T> RootNode { get; }
private Func<BinaryNode<T>, NodeMetadata<T>> NodeToMetadata { get; }
private Stack<BinaryNode<T>> UnprocessedNodes { get; }
private Stack<bool> LeftChildProcessed { get; }
private BinaryNode<T> CurrentNode { get; set; }
public InorderMetaEnumerator(BinaryNode<T> rootNode,
Func<BinaryNode<T>, NodeMetadata<T>> nodeToMetadata)
{
this.RootNode = rootNode;
this.NodeToMetadata = nodeToMetadata;
this.UnprocessedNodes = new Stack<BinaryNode<T>>();
this.LeftChildProcessed = new Stack<bool>();
this.PushIfExists(rootNode);
}
public NodeMetadata<T> Current
{
get
{
if (this.CurrentNode == null)
throw new InvalidOperationException();
return this.NodeToMetadata(this.CurrentNode);
}
}
object IEnumerator.Current
{
get
{
return this.Current;
}
}
public void Dispose()
{
}
public bool MoveNext()
{
if (this.UnprocessedNodes.Count == 0)
{
this.CurrentNode = null;
return false;
}
this.ExpandTop();
this.CurrentNode = this.UnprocessedNodes.Pop();
this.LeftChildProcessed.Pop();
this.PushIfExists(this.CurrentNode.RightChild);
return true;
}
public void Reset()
{
this.CurrentNode = null;
this.UnprocessedNodes.Clear();
this.LeftChildProcessed.Clear();
this.PushIfExists(this.RootNode);
}
private void ExpandTop()
{
while (this.ExpandSingleTop()) { }
}
private bool ExpandSingleTop()
{
if (this.LeftChildProcessed.Peek())
return false;
BinaryNode<T> node = this.UnprocessedNodes.Peek();
this.LeftChildProcessed.Pop();
this.LeftChildProcessed.Push(true);
PushIfExists(node.LeftChild);
return true;
}
private void PushIfExists(BinaryNode<T> node)
{
if (node == null)
return;
this.UnprocessedNodes.Push(node);
this.LeftChildProcessed.Push(false);
}
}
This class implements inorder iteration algorithm over the binary tree with specified root node. It implements the IEnumerator interface and can be used to traverse the binary tree.
Finally, the postorder enumerator is given below.
class PostorderMetaEnumerator<T> : IEnumerator<NodeMetadata<T>>
{
private BinaryNode<T> RootNode { get; }
private Func<BinaryNode<T>, NodeMetadata<T>> NodeToMetadata { get; }
private BinaryNode<T> CurrentNode { get; set; }
private Stack<BinaryNode<T>> UnprocessedNodes { get; }
private Stack<bool> AreChildrenPushed { get; }
public PostorderMetaEnumerator(BinaryNode<T> rootNode,
Func<BinaryNode<T>, NodeMetadata<T>> nodeToMetadata)
{
this.RootNode = rootNode;
this.NodeToMetadata = nodeToMetadata;
this.UnprocessedNodes = new Stack<BinaryNode<T>>();
this.AreChildrenPushed = new Stack<bool>();
this.PushIfExists(rootNode);
}
public NodeMetadata<T> Current
{
get
{
if (this.CurrentNode == null)
throw new InvalidOperationException();
return this.NodeToMetadata(this.CurrentNode);
}
}
object IEnumerator.Current
{
get
{
return this.Current;
}
}
public void Dispose()
{
}
public bool MoveNext()
{
if (this.UnprocessedNodes.Count == 0)
{
this.CurrentNode = null;
return false;
}
this.ExpandTop();
this.CurrentNode = this.UnprocessedNodes.Pop();
this.AreChildrenPushed.Pop();
return true;
}
private void ExpandTop()
{
while (this.ExpandSingleTop()) { }
}
private bool ExpandSingleTop()
{
if (this.AreChildrenPushed.Peek())
return false;
BinaryNode<T> node = this.UnprocessedNodes.Peek();
this.AreChildrenPushed.Pop();
this.AreChildrenPushed.Push(true);
this.PushIfExists(node.RightChild);
this.PushIfExists(node.LeftChild);
return true;
}
public void Reset()
{
this.CurrentNode = null;
this.UnprocessedNodes.Clear();
this.AreChildrenPushed.Clear();
this.PushIfExists(this.RootNode);
}
private void PushIfExists(BinaryNode<T> node)
{
if (node == null)
return;
this.UnprocessedNodes.Push(node);
this.AreChildrenPushed.Push(false);
}
}
Just for the sake of completeness, we can write part of the BinaryTree class which exposes three sequences – preorder, inorder and postorder – each in two flavors – raw data or metadata:
class BinaryTree<T>
{
...
public IEnumerable<T> GetPreorderSequence()
{
return this.GetSequence(this.GetPreorderMetaEnumerator());
}
public IEnumerable<T> GetInorderSequence()
{
return this.GetSequence(this.GetInorderMetaEnumerator());
}
public IEnumerable<T> GetPostorderSequence()
{
return GetSequence(this.GetPostorderMetaEnumerator());
}
public IEnumerable<NodeMetadata<T>> GetPreorderMetaSequence()
{
return this.GetMetaSequence(this.GetPreorderMetaEnumerator());
}
public IEnumerable<NodeMetadata<T>> GetInorderMetaSequence()
{
return this.GetMetaSequence(this.GetInorderMetaEnumerator());
}
public IEnumerable<NodeMetadata<T>> GetPostorderMetaSequence()
{
return this.GetMetaSequence(this.GetPostorderMetaEnumerator());
}
private IEnumerator<NodeMetadata<T>> GetPreorderMetaEnumerator()
{
return new PreorderMetaEnumrator<T>(this.RootNode, this.MetadataFor);
}
private IEnumerator<NodeMetadata<T>> GetInorderMetaEnumerator()
{
return new InorderMetaEnumerator<T>(this.RootNode, this.MetadataFor);
}
private IEnumerator<NodeMetadata<T>> GetPostorderMetaEnumerator()
{
return new PostorderMetaEnumerator<T>(this.RootNode, this.MetadataFor);
}
private IEnumerable<NodeMetadata<T>> GetMetaSequence(IEnumerator<NodeMetadata<T>> metaEnumerator)
{
while (metaEnumerator.MoveNext())
yield return metaEnumerator.Current;
}
private IEnumerable<T> GetSequence(IEnumerator<NodeMetadata<T>> metaEnumerator)
{
foreach (NodeMetadata<T> metadata in this.GetMetaSequence(metaEnumerator))
yield return metadata.Content;
}
private NodeMetadata<T> MetadataFor(BinaryNode<T> node)
{
return new NodeMetadata<T>(node,
(child) => this.HasParent(child),
(child) => this.GetParentMetadata(child));
}
}
Once again you can see how simple and straight-forward it is to return enumerators from a collection when enumerating algorithm is implemented in a separate class.
Externalizing enumerators is a convenient tactic to simplify the collection. Its drawback is that collection now has to expose part of its implementation so that the external enumerator could walk through its content. This doesn’t have to be so bad. We can manage the problem by exposing only the reasonable minimum of the collection’s implementation details, such as node structure, and leave the rest of its implementation private. Remember that any implementation leak means that the consumer will have more obligations than before. Keeping the class implementation private means that consumers have less to know about when using the class.
External Enumerator and Collection Versioning
In the previous section we have demonstrated benefits of moving enumeration algorithm to a separate class. Now that the other class is responsible to move between elements of the collection, a separate question raises. How do we guard against changes made to the collection content? The problem is obvious: Collection’s responsibility is to change its content; enumerator’s responsibility is to navigate between elements of the collection. These two responsibilities must be reconciled if we wanted to avoid runtime errors that occur if the consumer is changing the collection while iterating through it.
Note that we did not have this particular problem in previous section because there we were working with immutable tree nodes. In that case each enumerator effectively sees a snapshot of the data structure. As the result, it was not necessary to test the collection version from the enumerator.
But in general case we will still have to test collection version in each enumeration step. And, since the external enumerator does not have access to current collection version, it becomes obvious that the collection must engage and make its current version accessible to the enumerator. Let’s take the DynamicArray class as an example:
class DynamicArray<T>
{
private T[] array;
private int count;
public DynamicArray()
{
this.array = new T[0];
}
public void Append(T value)
{
this.ResizeToFit(this.count + 1);
this.array[this.count] = value;
this.count++;
}
public void RemoveAt(int pos)
{
if (pos < 0 || pos >= this.count)
throw new IndexOutOfRangeException();
for (int i = pos + 1; i < this.count; i++)
this.array[i - 1] = this.array[i];
this.count--;
this.Shrink();
}
private void ResizeToFit(int desiredCount)
{
int newSize = this.array.Length;
while (newSize < desiredCount)
newSize = Math.Max(1, newSize * 2);
System.Array.Resize<T>(ref this.array, newSize);
}
private void Shrink()
{
if (this.array.Length < this.count * 2)
return;
int newSize = this.array.Length;
while (newSize >= this.count * 2)
newSize = 2;
System.Array.Resize(ref this.array, newSize);
}
public IEnumerable<T> GetForwardSequence()
{
...
}
public IEnumerable<T> GetBackwardSequence()
{
...
}
}
This class wraps a common array, but the array is not always fully populated. The count field keeps track of how many elements are effectively stored in the array. When new elements are added, the array will be resized automatically. Conversely, when an element is removed from the collection, the underlying array will be shrunk.
The problem is when we want to implement GetForwardSequence() and GetBackwardSequence() methods, but in such way that the enumeration algorithm is implemented in a separate class. Here is the implementation we could start with:
class ArrayEnumerator<T> : IEnumerator<T>
{
private readonly T[] array;
private readonly int lowerIndex;
private readonly int upperIndex;
private readonly int increment;
private int currentIndex;
public ArrayEnumerator(T[] array, int fromIndex, int toIndex)
{
this.array = array;
this.lowerIndex = fromIndex;
this.upperIndex = toIndex;
this.increment = 1;
this.currentIndex = this.lowerIndex - 1;
if (fromIndex > toIndex)
{
this.lowerIndex = toIndex;
this.upperIndex = fromIndex;
this.increment = -1;
this.currentIndex = this.upperIndex + 1;
}
}
public T Current
{
get
{
if (this.currentIndex < this.lowerIndex ||
this.currentIndex > this.upperIndex)
throw new InvalidOperationException();
return this.array[this.currentIndex];
}
}
object IEnumerator.Current
{
get
{
return this.Current;
}
}
public void Dispose()
{
}
public bool MoveNext()
{
int nextIndex = this.currentIndex + this.increment;
if (nextIndex < this.lowerIndex ||
nextIndex > this.upperIndex)
return false;
this.currentIndex = nextIndex;
return true;
}
public void Reset()
{
this.currentIndex = this.lowerIndex - 1;
if (this.increment < 0)
this.currentIndex = this.upperIndex + 1;
}
}
This implementation supports forward and backward iteration over the array. It takes care of indexing through the array and everything is seemingly alright. We can use this enumerator class quite easily from the DynamicArray class:
class DynamicArray<T>
{
...
public IEnumerable<T> GetForwardSequence()
{
return this.GetSequence(
new ArrayEnumerator<T>(this.array, 0, this.count - 1));
}
public IEnumerable<T> GetBackwardSequence()
{
return this.GetSequence(
new ArrayEnumerator<T>(this.array, this.count - 1, 0));
}
private IEnumerable<T> GetSequence(IEnumerator<T> enumerator)
{
while (enumerator.MoveNext())
yield return enumerator.Current;
}
}
Once again it took only a few lines of code to expose two different enumeration algorithms through the collection class interface. But still there is the problem. Collection could change its content while there is an enumerator working on the same underlying array. Elements that appear on the enumerator’s output could easily differ from elements that are currently located in the collection.
If we wanted to protect the consumer from inconsistent data coming out of the GetBackwardSequence() and GetForwardSequence() methods, then we had to implement content versioning on the DynamicArray class. It would be sufficient to just allocate a number for this purpose:
class DynamicArray<T>
{
private T[] array;
private int count;
private long version;
public DynamicArray()
{
this.array = new T[0];
}
public void Append(T value)
{
this.ResizeToFit(this.count + 1);
this.array[this.count] = value;
this.count++;
this.version++;
}
public void RemoveAt(int pos)
{
if (pos < 0 || pos >= this.count)
throw new IndexOutOfRangeException();
for (int i = pos + 1; i < this.count; i++)
this.array[i - 1] = this.array[i];
this.count--;
this.Shrink();
this.version++;
}
...
}
One simple long variable does it all. Append() and RemoveAt() method must increment the version number before returning. In that way, we will be able to positively identify any change made to the content of the collection.
On the other end of the wire, we have the enumerator class. In order to detect changes made to the collection, the enumerator would have to know two things: Initial version which was in effect when the enumerator was created; and current version at the moment of moving to the next element of the array or accessing the array element.
The first part, knowing the initial version, is easy. We can just pass the current version to the enumerator when constructing it and enumerator can remember that version and use it in future operations.
But the second part, verifying that initial and current versions are the same, is a bit trickier. Current version is stored in the collection. Enumerator has no access to that information. One possible solution is to let the collection pass a special function to the enumerator, so that the enumerator can call that function whenever it has to check the version. Here is the modified enumerator class which implements this idea:
class ArrayEnumerator<T> : IEnumerator<T>
{
private readonly T[] array;
private readonly int lowerIndex;
private readonly int upperIndex;
private readonly int increment;
private int currentIndex;
private readonly long initialVersion;
private readonly Action<long> assertVersionIsEqualTo;
public ArrayEnumerator(T[] array, int fromIndex, int toIndex,
long initialVersion,
Action<long> assertVersionIsEqualTo)
{
this.array = array;
this.initialVersion = initialVersion;
this.assertVersionIsEqualTo = assertVersionIsEqualTo;
this.lowerIndex = fromIndex;
this.upperIndex = toIndex;
this.increment = 1;
this.currentIndex = this.lowerIndex - 1;
if (fromIndex > toIndex)
{
this.lowerIndex = toIndex;
this.upperIndex = fromIndex;
this.increment = -1;
this.currentIndex = this.upperIndex + 1;
}
}
public T Current
{
get
{
this.AssertVersion();
if (this.currentIndex < this.lowerIndex ||
this.currentIndex > this.upperIndex)
throw new InvalidOperationException();
return this.array[this.currentIndex];
}
}
object IEnumerator.Current
{
get
{
return this.Current;
}
}
public void Dispose()
{
}
public bool MoveNext()
{
this.AssertVersion();
int nextIndex = this.currentIndex + this.increment;
if (nextIndex < this.lowerIndex ||
nextIndex > this.upperIndex)
return false;
this.currentIndex = nextIndex;
return true;
}
public void Reset()
{
this.AssertVersion();
this.currentIndex = this.lowerIndex - 1;
if (this.increment < 0)
this.currentIndex = this.upperIndex + 1;
}
private void AssertVersion()
{
this.assertVersionIsEqualTo(this.initialVersion);
}
}
This is the complete listing of the ArrayEnumerator class which can assert versio number in all operations: getting the current element, moving to the next element, as well as reseting the enumeration. The feature is made possible by receiving two additional parameters through the constructor: Initial version number, and an action which will effectively assert that current version meets its argument and fail otherwise.
Once the enumerator class has been completed, it becomes very easy for us to use it from the DynamicArray collection. All it takes is to feed additional version-related arguments to the enumerator’s constructor:
class DynamicArray<T>
{
...
public IEnumerable<T> GetForwardSequence()
{
return this.GetSequence(this.CreateEnumerator(0, this.count - 1));
}
public IEnumerable<T> GetBackwardSequence()
{
return this.GetSequence(this.CreateEnumerator(this.count - 1, 0));
}
private IEnumerator<T> CreateEnumerator(int fromIndex, int toIndex)
{
return new ArrayEnumerator<T>(this.array, fromIndex, toIndex,
this.version,
this.AssertVersion);
}
private IEnumerable<T> GetSequence(IEnumerator<T> enumerator)
{
while (enumerator.MoveNext())
yield return enumerator.Current;
}
private void AssertVersion(long version)
{
if (this.version != version)
throw new InvalidOperationException("Collection has changed.");
}
}
Here we have this AssertVersion() method which implements the version checking functionality. The rest of the code is then straight-forward and it is all enclosed in the CreateEnumerator() method. Whenever a new enumerator is created to be returned to the client, current version and AssertVersion() function are passed for it to use.
Lesson learned from this example is that yet another piece of implementation has leaked out of the collection. We already saw before that externalizing the enumeration algorithm means that some of the data representation which was encapsulated in the collection class now becomes a common knowledge. Well, versioning the content becomes another part of previously well hidden, but now well known implementation detail. That is the price we pay if we want to have the benefits that come when enumeration is not implemented in the collection, but in a separate class instead.
If you wish to learn more, please watch my latest video courses

Beginning Object-oriented Programming with C#
In this course, you will learn the basic principles of object-oriented programming, and then learn how to apply those principles to construct an operational and correct code using the C# programming language and .NET.
As the course progresses, you will learn such programming concepts as objects, method resolution, polymorphism, object composition, class inheritance, object substitution, etc., but also the basic principles of object-oriented design and even project management, such as abstraction, dependency injection, open-closed principle, tell don't ask principle, the principles of agile software development and many more.
More...

Design Patterns in C# Made Simple
In this course, you will learn how design patterns can be applied to make code better: flexible, short, readable.
You will learn how to decide when and which pattern to apply by formally analyzing the need to flex around specific axis.
More...

Refactoring to Design Patterns
This course begins with examination of a realistic application, which is poorly factored and doesn't incorporate design patterns. It is nearly impossible to maintain and develop this application further, due to its poor structure and design.
As demonstration after demonstration will unfold, we will refactor this entire application, fitting many design patterns into place almost without effort. By the end of the course, you will know how code refactoring and design patterns can operate together, and help each other create great design.
More...

Mastering Iterative Object-oriented Development in C#
In four and a half hours of this course, you will learn how to control design of classes, design of complex algorithms, and how to recognize and implement data structures.
After completing this course, you will know how to develop a large and complex domain model, which you will be able to maintain and extend further. And, not to forget, the model you develop in this way will be correct and free of bugs.
More...
About

Zoran Horvat is the Principal Consultant at Coding Helmet, speaker and author of 100+ articles, and independent trainer on .NET technology stack. He can often be found speaking at conferences and user groups, promoting object-oriented and functional development style and clean coding practices and techniques that improve longevity of complex business applications.
Elsewhere
Video Courses
- Making Your C# Code More Object-oriented
- Beginning Object-oriented Programming with C#
- Collections and Generics in C#
- Design Patterns in C# Made Simple
- Refactoring to Design Patterns
- Mastering Iterative Object-oriented Programming in C#
- Making Your C# Code More Functional
- Making Your Java Code More Object-oriented
- Writing Purely Functional Code in C#
- Tactical Design Patterns in .NET: Creating Objects
- Tactical Design Patterns in .NET: Control Flow
- Tactical Design Patterns in .NET: Managing Responsibilities
- Advanced Defensive Programming Techniques
- Writing Highly Maintainable Unit Tests
- Improving Testability Through Design
Articles
- Here is Why Calling a Virtual Function from the Constructor is a Bad Idea
- What Makes List<T> So Efficient in .NET?
- Nondestructive Mutation and Records in C#
- Understanding Covariance and Contravariance of Generic Types in C#
- Using Record Types in C#
- Unit Testing Case Study: Calculating Median
- More...