What Makes while Loop a Poor Choice in Programming

by Zoran Horvat
May 08, 2018

When it comes to looping through objects or values, we have several choices. A for loop; a foreach loop; a while loop; a do..while loop. And usually, we have some sequence-processing library or syntax at our disposal. In .NET languages, we have the LINQ library available to process any sequence without having to loop explicitly.

These looping methods are obviously not the same. But they are not equally powerful, either. In this article, I will question the usefulness of while loops (including do..while) and try to point you in the direction of not using them.

This opinion is biased, which asks for some explanation. I will be questioning the while loops from the ground of our ability to produce correct code. Therefore, the main argument in this article will be code correctness – number of bugs if you will - while other aspects will be of lesser importance. Most importantly, performance considerations will be ignored. Practice shows that all looping methods mentioned above (for/foreach loop, while loops and sequence processing libraries, like LINQ) perform similarly and therefore performance will not be improved by choosing one looping method over the other.

While Loop Might Never End

The principal complaint about while loops is that they may never end:

while (true)
{
  ...
}

This is the infinite loop. If it ever happens that you construct an infinite loop in code, that code will become non-responsive at run time.

The problem with infinite loops is not trivial, as it is in the code segment above. What I called true in the while loop’s condition will usually be more complex:

while (condition || anotherOne)
{
  ...
}

If at any point during the program’s execution one of the conditions became terminally True, then the loop will turn into an infinite loop. Programmers are often unable to notice this problem by code inspection alone.

For Loop Might Never End, Too

Please note that for loop alone does not differ from the while loop. Namely, for loop’s syntax consists of three components which can easily be transformed into the while loop form.

for (Initialize();
     ShouldContinue();
     ReevaluateConditions())
{
  ...
}

This for loop brings nothing new to the table compared to while:

Initialize();
while (ShouldContinue())
{
  ...
  ReevaluateConditions();
}

Therefore, the for loop syntax alone will not save you from infinite loop bug. It gets a little better if you use it in its idiomatic form:

for (int i = 0; i < n; i++)
{
  ...
}

While this code only represents a special case of the general for loop syntax, it is still safer than any other example given above, simply because it is idiomatic. Lest you try to modify the iterator variable i inside the loop, which you should never do anyway, you’ll be safe from infinite iteration.

However, this form of the for loop is rarely useful today. Usually, you will have to include a more complex exit condition, like in this example:

for (Car car = parking.ClosestCar();
     car.Color != Colors.Red; 
     car.Paint())
{
  ...
}

As in the case of the while loop, the exit condition of this for loop might never be satisfied, turning it into an infinite loop.

Understanding Loops

Every loop must end. That is also known as the loop termination condition, and it is very easy to understand. Any loop can be represented as a while loop with a Boolean condition in its head:

while (condition)
{
  ...
}

For a loop to be valid, the condition must at some point turn False. That is what we call the termination condition – there must be a proof that the loop will not run forever.

On the other hand, for a loop to be part of an algorithm, we would introduce its preconditions, postconditions and invariants. Preconditions are the Boolean conditions that must be satisfied before entering the loop. Postconditions are the Boolean conditions satisfied by the result obtained when the loop terminates. And invariants are the Boolean conditions that must be satisfied at all times, before, and after the loop, as well as after every iteration of the loop.

Let’s take an example. Consider a loop which finds maximum value in an array:

int max = a[0];
for (int i = 1; i < a.Length; i++)
{
  if (a[i] > max)
  {
    max = a[i];
  }
}

How can we prove that this loop will indeed produce the maximum value? It is really easy if you think it through: Define the postcondition, which says that the result is the maximum value, and define the termination condition, which says that the loop will terminate, and execution reach the point at which the result can be produced.

Therefore, we have the loop postcondition:

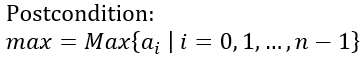
Termination condition is the second part of the infrastructure, and it says that at some point, exit condition will be satisfied:

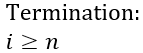
Now we need to prove that both conditions are satisfied, and that will be the formal proof that this loop indeed produces a maximum value of an array.

But that is not all we have to do. We must also specify the preconditions, i.e. conditions that must be met before the loop begins. If preconditions are violated, then we suspect that the loop wouldn’t be able to evaluate its body in the first place. You may have already noticed that the max variable is initialized to the first value in the array. For this operation to succeed, we must ensure that the array contains at least one value:

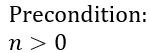
We’re getting closer to the solution with every step of the way. The last element in this puzzle is the loop invariant. That is where we usually need a bit of imagination. Loop invariant can help prove that no data structure will ever be broken, that all arithmetic operations will be possible, and so on. But you can also use loop invariant to help you explain the algorithm and then use that formal explanation to prove correctness of the postcondition.

Here is the loop invariant which fits firmly with the code:

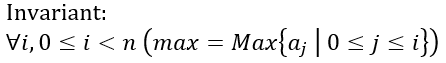
To cut the long story short, this invariant says that at the end of any iteration of the loop, the max variable contains the maximum value between the beginning of the array and the just visited position in the array.

Bottom line is that maximum value loop, and the entire maximum value algorithm for that matter, is entirely defined with these four conditions, which must be proven correct before concluding that the algorithm and the loop are correct:

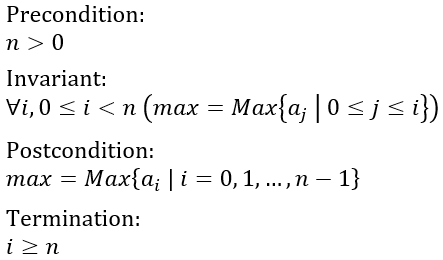
I will not bother to prove these conditions here, as I feel that we have already drifted too far away from the main topic. I would ask you to fill in the gaps as the exercise. You can start from observation that the loop variable i is strictly increasing with every iteration, and therefore termination condition will be satisfied at some point.

Also, with precondition satisfied (and you can take that for granted), and knowing the law by which loop variable increases, you can reach and inductive proof that loop invariant will be satisfied indeed at the end of every iteration.

Finally, you will observe that the loop invariant reads the same as the postcondition when end of the loop is reached. By following these steps, you will prove that the algorithm and the loop are both terminating and producing the expected result in every possible case.

And now back to the main topic of this article: Loop termination. For every loop you write, you must be sure that its termination condition will be satisfied after finite number of iterations. Without that proof, the loop will be open for bugs, and such bugs will manifest in endless execution of the loop.

How Can Sequences Help with Loop Termination?

Working with sequences is quite different from implementing loops. The main difference is that the loop itself will now be transformed in such way that termination condition disappears entirely.

The foreach loop is designed to work with sequences in C#. Let’s rewrite the maximum value for loop into its foreach counterpart:

int max = a[0];
foreach (int x in a)
{
  if (x > max)
  {
    max = x;
  }
}

This algorithm is a bit different than the previous one (I’ll leave it to you to find the difference). But it can still be described with similar preconditions, postconditions, invariants and the termination condition.

Can you tell what termination condition will be here?

Here is how we could define it: The foreach loop reaches the last element in a. We don’t have access to the loop’s internal workings, and therefore we can only tell that it will terminate if there is an element in a which is not followed by another element.

And now that that is clear, we can reformulate the termination condition and say: The foreach loop will terminate if and only if applied to a finite sequence.

This sounds more practical. You can tell that every foreach loop will terminate as long as you have finite sequences in your hands.

How Can LINQ Help with Loop Conditions?

And so, we arrive at LINQ. It is the library which defines operators defined on sequences, where sequence is formally defined as an object implementing the IEnumerable<T> interface. Let’s rewrite the maximum value example again, this time to use the LINQ Aggregate operator:

int max = a.Aggregate((acc, cur) => cur > acc ? cur : acc);

This is something completely different, compared to while and foreach loops we saw this far. Yet, we can still define all conditions as before. There, we find loop precondition to read the same as before, as the sequence a must contain at least one element. Otherwise, Aggregate operator would fail to initialize. Loop invariant is that after every iteration the acc variable contains the maximum value of all the values visited this far. Loop postcondition is that at the end of the iteration, the acc variable contains the overall maximum value.

And lastly, termination condition will say that the Aggregate operator will have to exhaust all elements in the sequence to terminate. In other words, we are meeting the same termination condition again: The input sequence must be finite.

Wrapping Up the Theory with Sequences

When sequences and LINQ are used, we recognize that places where conditions are defined have been changed. That is the most remarkable observation about loops. Precondition and termination condition will be defined on the sequence. Sequence consumer will have no responsibilities there. Invariant and postcondition, on the other hand, will remain entirely on the consuming end.

In the example above, precondition (sequence is not empty) and termination condition (sequence is finite) are both defined on the sequence itself. The rest of the conditions is what the lambda passed to the Aggregate operator will be responsible to ensure.

And now we can think how that changes our position? If we write both ends of the code – initializing the sequence and then using it in the LINQ expression – then what is the benefit of this separation of concerns? Let’s add one line more to the implementation and then everything will fit into place:

IEnumerable<int> a = FetchData();
int max = a.Aggregate(
  (acc, cur) => cur > acc ? cur : acc);

Now it becomes more obvious. There are two segments of code involved here. One is the code which generates the sequence of objects. The other half is the LINQ expression which consumes the sequence.

That is how new separation of concerns comes to the table. It is the data generator’s responsibility to ensure the precondition and termination condition. It is then the data consumer’s responsibility to implement the algorithm on those data, and that means to satisfy the loop invariant and the postcondition.

The algorithm is none of our business, if you think it through. Generally, the algorithm is the solution to the problem, and we are solving it the way we usually do that. Invariants and postconditions are merely a mathematical tool we use. However, algorithm implementation can make a call to a non-terminating function. That means that part of the termination condition still exists in the lambda expression used in LINQ. However, in nearly any practical situation, a moment of code inspection would be sufficient to discover whether the lambda terminates or will hang forever.

That leaves us with only the data generator where we are free to do the things in one way or the other. That is exactly where preconditions and termination condition are gaining importance. It is very useful to know, at that point where we are asked to satisfy these two conditions while generating data, that termination condition has turned into a trivial question: Is the sequence finite? If it is, then we are fine. Otherwise, we are not fine.

Return to the beginning of this article and you will see that nearly every loop had a different termination condition, and these conditions were nearly always mixed together with logic inside the loop. With sequences and LINQ, and even with the foreach loop, all that diversity is gone, replaced with one and only universal condition – every loop on a sequence will be terminated in finite number of iterations if it doesn’t contain an infinite operation and the sequence is finite.

Once again, the fact that the lambda always terminates will usually be trivial to prove. That leaves us with the simple condition that the sequence must be finite and then the loop will never be stuck.

A Word About API Design

There is one side-effect of the conclusions we have drawn this far. It gives us a hint about good API design. Imagine a task of designing the data generator, the entity which produces data over which the consumer will loop. How exactly would you approach that task?

Let’s revisit the example with cars and their colors again:

for (Car car = parking.ClosestCar();
     car.Color != Colors.Red;
     car.Paint())
{
  ...
}

We have already concluded that this design is risky because Paint method on the Car object would have to guarantee that it will eventually reach the red color. Will it or will it not, that is beyond comprehension of this loop. Therefore, the loop, however correct by itself, might never terminate thanks to conditions that are expressed someplace else.

Could you come up with a better design, now that you understand loop conditions?

For one thing, we could turn this API into a form based on IEnumerable – the sequence of Car objects this time. Consider this design:

parking.ClosestCar()
  .ProducePaints()
  .TakeWhile(car => car.Color != Colors.Red)
  .Select(car => ...);

The difference this design brings is that loop termination condition now boils down to knowing that the ProducePaints method returns a finite sequence, and nothing more than that. Even if the red car was never produced, the loop will eventually terminate when all the paint colors have been tried out.

The ProducePaints method can even return a lazy-evaluated sequence (which is the preferred method, anyway). That would ensure that performance will not be affected by the overall length of the sequence, but only by the demand of the subsequent chained operators.

This can be used as the general guideline when designing classes and libraries. Return sequences. Avoid protocols and methods returning flags.

Summary

In this article we have examined basic properties of loops and put them in perspective of two orthogonal approaches to looping: Common loop syntax, like for, while and do..while loops on the one hand, and LINQ and sequences, with addition of the foreach loop on the other.

The result of this thorough examination is that the prior methods, common loops, are prone to infinite loop bugs. It is important to prove, in every separate case, that the loop will eventually terminate, besides proving that it will produce the result which was expected.

The same problem, loop termination, diminishes to a trivial condition when data over which the loop execute are organized into a sequence, an IEnumerable<T>. In that case, all we have to do is ensure that the sequence is finite, and the loop will terminate for sure.

In the end, we have touched the question of designing APIs. Lead by the desire to simplify the consuming end, the one which initiates the loop iteration, we conclude that the good API is the one which exposes a sequence of data, rather than any other loop-friendly design. As long as the API can produce a finite sequence, we conclude that its consumer will be safe from infinite loops no matter how clumsily it might behave on its end.

---