Why do We Need Guard Clauses?

by Zoran Horvat
August 18, 2015

Motivation Behind Guard Clauses

Guard clauses are among the best known idioms across many programming languages. Syntax differs, but the idea behind remains the same:

class ShoppingCart
{
    void Add(IProduct item)
    {
        if (item == null)
            throw new ArgumentNullException("item");
        ...
    }
}

In this brief example, we are implementing the shopping cart class. Its Add method is responsible to add a product to the cart. Should the caller pass null reference to the shopping cart, the Add method throws ArgumentNullException back. This idiom is a well-known If-Then-Throw pattern.

But don’t let this if-null-throw example distract your attention from a more general principle. Imagine in the same shopping cart example that some products are not available for sale yet. They might exist in the database for future use, but right now they cannot be purchased. If client code has attempted to add such a product to the cart, the cart should throw an exception back at it. Here is another guard clause doing precisely that:

class ShoppingCart
{
    void Add(IProduct item)
    {
        if (item == null)
            throw new ArgumentNullException("item");

        if (!item.IsOfferedForSale)
            throw new ArgumentException("Item cannot be added to cart.");
        ...
    }
}

Have you ever considered why we are writing code like this? Isn’t there a different, if not better approach?

In this article we will tackle the question of guarding against invalid input from a different perspective and see where it will take us.

Introducing Functions

At Math World website we find a definition of a function as follows: A function is a relation that uniquely associates members of one set with members of another set.

In this respect, object-oriented approach comes handy, since types already define sets of their corresponding objects. Back to the example with shopping cart, where we had Product and ShoppingCart types. Adding a product to a shopping cart means to map a shopping cart and a product on one side to a new shopping cart on the other side, as shown in the following picture.

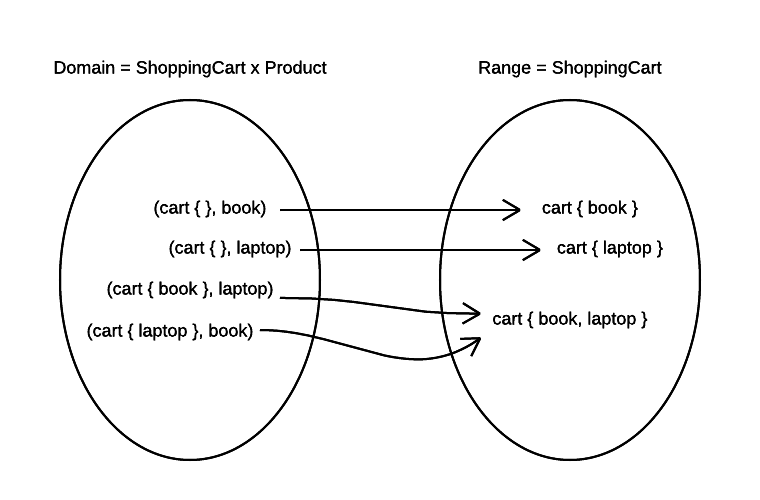
Here we can see how the Add function operates. It is run on a shopping cart and it receives a product. Consequently, domain of this function is a Cartesian product of sets of all possible shopping carts and all possible products. On the other hand, range of the function (set to which function maps elements of the domain) is just a set of all possible shopping carts. Mapping is performed so that a shopping cart together with the new product gets mapped to a new instance of the shopping cart, with new product added to whatever it already contained.

In the picture above, you can see that a pair consisting of an empty shopping cart and a laptop maps to a shopping cart which contains a laptop. Similarly, shopping cart which contains a book and a laptop map to a shopping cart containing both a book and a laptop. Note that the last pair indicates that shopping cart containing a laptop and a book map to the same shopping cart as the previous pair.

So much so about mapping objects to new objects. Where is the problem then? The problem comes when certain elements of the domain map to nothing.

Introducing Partial Functions

The next image shows a domain with one additional pair – product in this example is null. You can see the added pair at the bottom of the domain set.

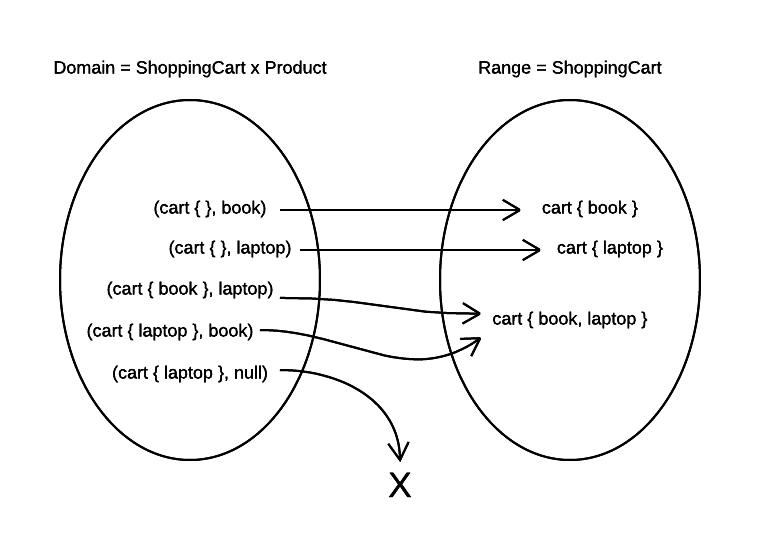
This pair from domain doesn’t map to any element in the range set. That is the root cause of all our problems – in order to call mapping a function, it must define mapping for every element of the domain. Not a single element must be missing in the mapping definition.

To make things worse, we come up with more elements that cannot be mapped. Remember the shopping cart requirement? Some products are not available for sale yet.

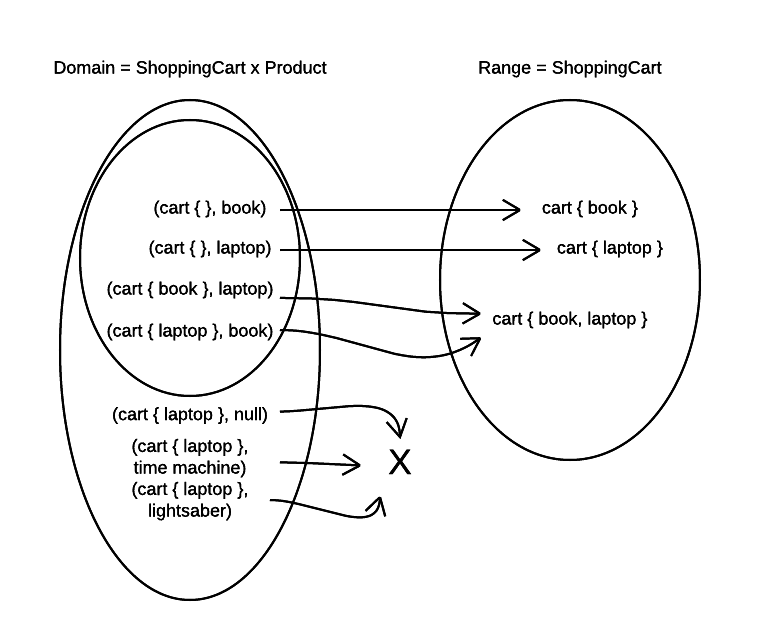
With this last set diagram we come to precisely identifying the problem. Domain of the function is not the complete Cartesian product of types involved. Some pairs are missing and cannot be mapped to the range.

When function is defined on part of a certain domain, it is called partial. Add method of the shopping cart is partial function because it doesn’t accept some products. Notably, null reference is not part of the method’s domain. And so are all the non-null product objects that claim to not be for sale.

Now that we have identified the root cause of our discomfort, we can try to address it.

Possible Solution to Avoid Partial Functions

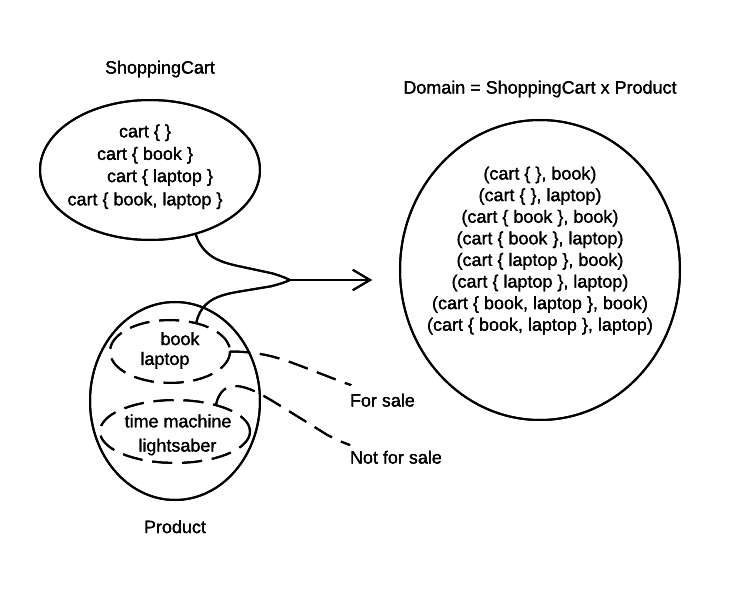
One method that is generally applicable, and should be applied when possible, is to avoid partial functions altogether. The domain of the Add method in the shopping cart example was constructed as a Cartesian product of all shopping carts and all products in the database, as shown in the picture below.

This way of defining the domain is the problem in its own right. As you can see in the picture, Product set consists of two disjoint subsets – those products that are offered for sale and those that are not.

Part of our troubles came from the fact that products not for sale, such as time machine, were included in the Add method domain. Now that the image shows these products as a separate subset, it becomes quite obvious that these products should be moved out.

This idea yields a smaller domain with better focus. Practical advice from this example would be: Try not to define the domain too broad. Let the method implementation define the domain on which it can be defined. Then, design types that are aligned with the desired domain.

Implementing the Domain in Code

It is rather simple to implement a type that defines a reduced domain. To see how to do that, we can start from the IProduct interface which did not do that right:

interface IProduct
{
    string Name { get; }
    bool IsOfferedForSale { get; }
    decimal Price { get; }
}

This piece of code clearly indicates the problem. There we have a Boolean property named IsOfferedForSale which makes a semantic distinction between two subsets of the set of all products. And the consequence of this design was the need to guard against instances of IProduct that return False from this property:

class ShoppingCart
{
    void Add(IProduct item)
    {
        ...
        if (!item.IsOfferedForSale)
            throw new ArgumentException("Item cannot be added to cart.");
        ...
    }
}

It would be better if we could separate two kinds of products so that the function implementation doesn’t have to test the flag. And, thanks to the Interface Segregation Principle, we can do precisely that:

interface IProduct
{
    string Name { get; }
}

interface IProductForSale : IProduct
{
    decimal Price { get; }
}

We have introduced a specialized product – that which can be offered for sale. IProductForSale defines a subset of IProduct type. Note that this design change has caused other changes to appear immediately. The Boolean flag has gone from the IProduct interface definition. And the Price property has moved down to the IProductForSale interface. The latter change was induced by the notion that the product doesn’t have a price until it can be offered to buyers.

But the most important change is yet to happen. Function implementation, impersonated in the Add method of the ShoppingCart class, will now be able to receive a reduced domain:

class ShoppingCart
{
    void Add(IProductForSale item)
    {
        if (item == null)
            throw new ArgumentNullException("item");

        //if (!item.IsOfferedForSale)
        //    throw new ArgumentException("Item cannot be added to cart.");
        ...
    }
}

Guard clause which used to cut off input parameters that do not fit the partial domain is now gone. There is no partial domain anymore. All products that can be sent to the Add method are now valid and acceptable.

In mathematical terms, the Add method has become total, rather than partial function.

Almost. On the second look, there still is this guard against null remaining, which indicates that the method is still partial.

The Menace of Null

In the previous section we have seen how the method can restrict its parameters to fit the domain exactly. On the other hand, it turns that all reference types yield an extended set of possible values, null being an equal member of the set. This unfortunate situation is shown in the following picture.

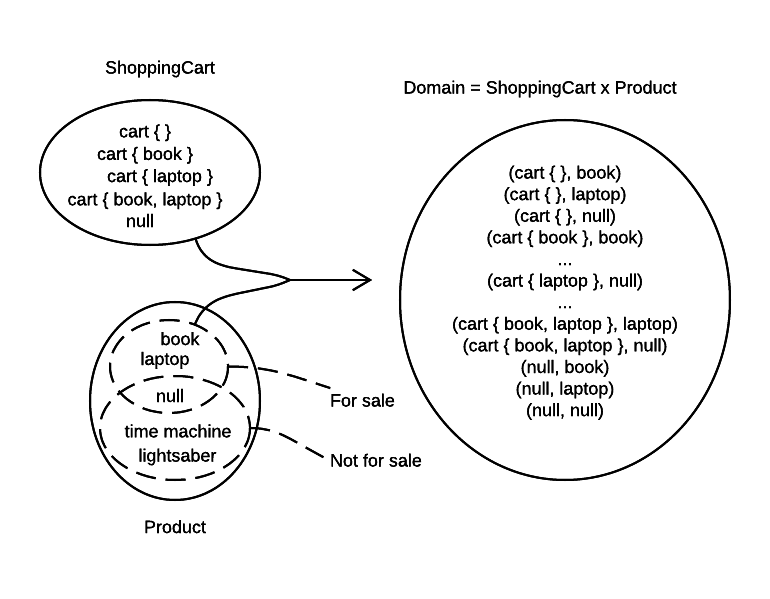
Now that both the product and the shopping cart can be null, we have new members of the domain. There are a few of them where shopping cart reference is null. We don’t have to guard against these cases because runtime will ensure that no code is executed when the parent object is null. This is not to say that we don’t have a problem – we do, and client execution will fail with NullReferenceException on our behalf.

But even when the shopping cart is not null, we have members of the domain where product is null. That is the case that makes our Add method partial again. In other words, guard clause against null must always remain in methods because null reference is a valid, yet semantically not acceptable member of the domain.

The most that we can get is to have function implementation that looks something like this:

class ShoppingCart
{
    void Add(IProductForSale item)
    {
        if (item == null)
            throw new ArgumentNullException("item");

        // Actual work...
    }
}

Conclusion

In this article we have discussed the question of function domains. We have seen that every method we implement can be viewed as a mathematical function. In that respect, the method is defined on a certain domain, a set consisting of objects, and it maps its result to a (potentially the same) set called range.

The problem that naturally occurs in programming is that the method is not defined on its complete domain. In order to implement the method, we have to guard against elements of the domain that are not covered by the mapping. That is what guard clauses are used for.

But there is the bright side of the story, too. We don’t have to guard a lot. In many practical cases, it is possible to introduce subtypes that precisely cover the domain of the function. That makes the method implementation complete, or total in mathematical terms.

With that change, only the null references remain to be guarded against. The mere existence of null references guarantees that all methods implemented on reference types will be partial by definition.

---