Finding a Value in a Sorted Array
by Zoran Horvat
Problem Statement
Given a sorted array of integer numbers, write a function which returns zero-based position on which the specified value is located. Function should return negative value if requested number cannot be found in the array. If value occurs more than once, function should return position of the first occurrence.
Example: Suppose that array consists of numbers 2, 3, 5, 6, 6, 8, 9. If value 6 is searched, then result is 3, because that is the zero-based position of the first occurrence of number 6 in the array. If number 7 is searched, then result is a negative value (e.g. -1), which indicates that value 7 cannot be found in the array.
Keywords: Array, sorted, search, partitioning.
Problem Analysis
For a moment forget that array might contain the requested number more than once. If we reach a satisfactory algorithm that efficiently finds any occurrence of a number, then we will already be close to the solution. With a simple tweak we will then ensure that algorithm discovers the first occurrence of the number.
The simplest way to see if an array contains a requested value is to iterate through the array and stop as soon as the value is located. Alternatively, search fails if end of array is reached. This algorithm, with some enhancements, is demonstrated in one of the previous exercises ( Finding a Value in an Unsorted Array ). But this approach does not take advantage of the fact that array is sorted. In order to make the searching function faster, we will have to collect additional information about values in the array from the sort order itself.
If we take the array from example above and try to find number 6 in it, then we might inspect the first value (2) and conclude that search should continue forward because this value is less than the number we are looking for. But we are not constrained to iterate through the array too stringently. We could jump two positions ahead, where number 5 is located - still too small. Should we jump three steps ahead next time, we would find value 8, which is too large - signal to step back. And there we go - one position back and value 6 is found.
Searching tactic just demonstrated is not the most elegant one that we could come up with. But it hits the point in searching through the sorted array. We are free to jump back and forth through array as long as searching space shrinks with each step. After the first two comparisons we were sure that number 6 does not appear on any of the three leading positions. One step later, we already knew that number we are looking for doesn't appear on the last two positions either. In only three comparisons we have eliminated five out of seven elements of the array. This analysis shows that searching through the array can be much more efficient than the simple iterative approach when array is known to be sorted. Next thing to do now is to discover a better method of eliminating unwanted elements.
Suppose that we use an arbitrary method to pick a position in the array and to compare a number on that position, whichever it is, with the target number. If the two numbers are equal, then the search is over. Otherwise, we must decide on which side of the current position could the requested number be located. If current element is greater than the requested number, then searching should obviously continue on the left-hand part of the array. Otherwise, we continue searching on the right-hand part of the array. Algorithm continues recursively on the selected sub-array, completely discarding all the values on the other side of the element which was tested. Algorithm terminates either when element under test is equal to the number we are looking for, or when remaining section of the array becomes empty, in which case we simply conclude that the number was not located.
Now we are ready to ask the central question. At any given step we have a certain range within the array which we are investigating. All elements to the left and to the right have already been discarded. Without any additional information about values in the remaining section, which is the most convenient element we might choose for comparison to maximally reduce the search section?
Since requested value could be located anywhere within the array section (if it is there, in the first place), then the best we could do is to pick an element in the middle of the array, cutting the segment into equal halves (off by one, at most). That partitioning method guarantees that one half of the values will be gone once the comparison is done, whichever the comparison result.
Here is the pseudo-code which finds any occurrence of the requested value within the array:
function FindAnySorted(a, n, x)
a - sorted array
n - length of the array
x - value searched in the array
begin
left = 0
right = n – 1
while left <= right
begin
middle = (left + right) / 2
if a[middle] = x then
return middle
if a[middle] > x then
right = middle - 1
else
left = middle + 1
end
return -1 -- value was not found
end
Observe how the remaining part of the array reduces by half plus the middle element in each iteration of the algorithm. This leads to a conclusion that number of comparisons needed to find a value in the sorted array with N elements is proportional to logN in the worst case.
Now we should return to the original problem statement and try to modify the solution so that it returns position of the first occurrence of a value within the array in cases when that value occurs more than once. Modified partitioning algorithm would be to search for the boundary, a location between two elements, rather than a particular element, such that all numbers to the left of the boundary are strictly less than the requested number and all elements to the right are greater or equal to the requested number. With the example array from the problem statement (2, 3, 5, 6, 6, 8, 9), when searching for value 6, this boundary would fall between positions 2 and 3.
In the simple partitioning algorithm, we tracked positions left and right, which indicated the first and the last element in the remaining segment of the array, respectively. That way of tracking the elements was natural in that case, because array had to be non-empty in each step. Should the array become empty, the search would fail. In the modified solution, however, we are forcing the algorithm to run until remaining segment is empty. Its left and right border would then be the last element less than and the first element greater or equal than the requested element. This implies that initial left and right indices are -1 and N for zero-based array. In other words, initial boundaries will be outside the array. To picture this situation, we might imagine that there exists one infinitely small element to the left of the array occupying location -1, and one infinitely large element to the right of the array occupying location N. These two fake elements will certainly be the smallest and the largest elements in the array, and array will remain sorted. Note that left and right indicator in this setting now point outside of the current array segment. Algorithm will terminate when right indicator is by one position to the right of the left indicator.
The following picture demonstrates finding the first occurrence of number 6 within an array.
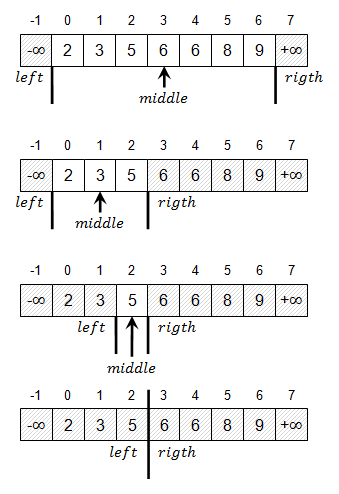
Observe how left and right indicators gradually converge towards each other. Once they meet, the cutting line between them divides the array – all values to the left are strictly less than 6; all values to the right are greater or equal to 6. Now the only thing remaining is to test whether there is any element to the right (cutting line could easily fall at the end of the array) and, if there is such an element, to test whether it is equal to 6. Since right-hand elements are greater or equal to 6, the first element to the right might as well be strictly greater than 6, in which case we simply conclude that searched number does not appear in the array.
Now that we have outlined the way in which bounds of the current array segment are tracked, we are ready to produce the final algorithm. Here is the pseudo-code:
function FindFirstSorted(a, n, x)
a - sorted array
n - length of the array
x - value searched in the array
begin
left = -1
right = n
while right > left + 1
begin
middle = (left + right) / 2
if a[middle] < x then
left = middle
else
right = middle
end
if right < n and a[right] = x then
return right
return -1
end
There are a couple of interesting details in this solution. First of all, we might ask is the while loop going to terminate in all cases? We are supposed to prove that middle is strictly greater than left and strictly less than right. If so, then in either way one of the boundaries is going to change and array segment being searched is going to shrink in every step. Proof for this claim is very simple if we start from the condition in the while statement:
right > left + 1
From this analysis we conclude that:
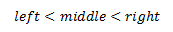
This proves that remaining part of the array is going to be shorter with every step of the algorithm. Middle position is strictly greater than left and strictly less than right boundary. As a result, either the left boundary is going to move to the right or the right boundary is going to move to the left. In either case, number of elements in between will reduce. Off course, once there are no more elements between the boundaries, the remaining part of the array will become empty and while loop will terminate.
Now that we know the function is going to exit at some point in time, we will examine the final part, in which return value is decided. Namely, the whole purpose of the loop was to find a dividing point in the array, a point standing in between the two elements, such that all numbers to the left are strictly less than the requested element and all numbers to the right are greater or equal to the requested element. The point to note here is that, once the loop terminates, variable right points to the first element of the array that is greater or equal to the searched number. Now there are two pitfalls out there. First one is that variable right might point outside the array (right = N). This happens if right remains with its initial value, which in turn happens when all values in the array are strictly less than the searched value. The second issue is if value at position right is not equal to the requested number. In that case, the loop has established a cutting point where smaller values end and larger values begin. There is nothing wrong with the loop, only there are no values equal to the searched number. Therefore, algorithm terminates with success only if the following combined criterion is met:
right < n and a[right] = xImplementation
With all the previous analysis, implementation of the function that finds first occurrence of a number in the sorted array is very simple. Here is the source code:
int FindFirstSorted(int[] a, int x)
{
int left = -1;
int right = a.Length;
while (right > left + 1)
{
int middle = (left + right) / 2;
if (a[middle] >= x)
right = middle;
else
left = middle;
}
if (right < a.Length && a[right] == x)
return right;
return -1;
}
Demonstration
Below is the source code of a simple console application which demonstrates use of the FindFirstSorted function.
using System;
namespace FindSortedDemo
{
public class Program
{
static Random _rnd = new Random();
static int[] GenerateArray(int n)
{
int[] a = new int[n];
for (int i = 0; i < n; i++)
a[i] = _rnd.Next(10);
Array.Sort(a);
return a;
}
static void PrintArray(int[] a)
{
for (int i = 0; i < a.Length; i++)
Console.Write("{0,3}", a[i]);
Console.WriteLine();
}
static int FindFirstSorted(int[] a, int x) { ... }
static void Main(string[] args)
{
while (true)
{
Console.Write("n=");
int n = int.Parse(Console.ReadLine());
if (n <= 0)
break;
int[] a = GenerateArray(n);
PrintArray(a);
Console.Write("x=");
int x = int.Parse(Console.ReadLine());
int pos = FindFirstSorted(a, x);
if (pos < 0)
Console.WriteLine("Value not found.");
else
Console.WriteLine("Value found at position {0}.", pos);
}
Console.Write("Press ENTER to continue... ");
Console.ReadLine();
}
}
}
When application is run, it produces output like this:
n=10
0 0 1 3 3 5 6 7 8 8
x=5
Value found at position 5.
n=7
0 2 3 3 7 8 9
x=1
Value not found.
n=9
0 1 2 4 4 5 6 8 8
x=9
Value not found.
n=8
2 2 2 2 3 4 8 9
x=2
Value found at position 0.
n=10
1 2 4 4 5 5 6 6 8 9
x=9
Value found at position 9.
n=0
Press ENTER to continue...
Follow-Up Exercises
Starting from the solution from this exercise, try to solve the following problems:
- Write the function which returns last occurrence of a number within the array.
- Write the function which simultaneously returns first and last occurrence of a number within the array. Try to optimize the search so that the function does not operate twice on the whole array.
If you wish to learn more, please watch my latest video courses

Beginning Object-oriented Programming with C#
In this course, you will learn the basic principles of object-oriented programming, and then learn how to apply those principles to construct an operational and correct code using the C# programming language and .NET.
As the course progresses, you will learn such programming concepts as objects, method resolution, polymorphism, object composition, class inheritance, object substitution, etc., but also the basic principles of object-oriented design and even project management, such as abstraction, dependency injection, open-closed principle, tell don't ask principle, the principles of agile software development and many more.
More...

Design Patterns in C# Made Simple
In this course, you will learn how design patterns can be applied to make code better: flexible, short, readable.
You will learn how to decide when and which pattern to apply by formally analyzing the need to flex around specific axis.
More...

Refactoring to Design Patterns
This course begins with examination of a realistic application, which is poorly factored and doesn't incorporate design patterns. It is nearly impossible to maintain and develop this application further, due to its poor structure and design.
As demonstration after demonstration will unfold, we will refactor this entire application, fitting many design patterns into place almost without effort. By the end of the course, you will know how code refactoring and design patterns can operate together, and help each other create great design.
More...

Mastering Iterative Object-oriented Development in C#
In four and a half hours of this course, you will learn how to control design of classes, design of complex algorithms, and how to recognize and implement data structures.
After completing this course, you will know how to develop a large and complex domain model, which you will be able to maintain and extend further. And, not to forget, the model you develop in this way will be correct and free of bugs.
More...
About

Zoran Horvat is the Principal Consultant at Coding Helmet, speaker and author of 100+ articles, and independent trainer on .NET technology stack. He can often be found speaking at conferences and user groups, promoting object-oriented and functional development style and clean coding practices and techniques that improve longevity of complex business applications.
Elsewhere
Video Courses
- Making Your C# Code More Object-oriented
- Beginning Object-oriented Programming with C#
- Collections and Generics in C#
- Design Patterns in C# Made Simple
- Refactoring to Design Patterns
- Mastering Iterative Object-oriented Programming in C#
- Making Your C# Code More Functional
- Making Your Java Code More Object-oriented
- Writing Purely Functional Code in C#
- Tactical Design Patterns in .NET: Creating Objects
- Tactical Design Patterns in .NET: Control Flow
- Tactical Design Patterns in .NET: Managing Responsibilities
- Advanced Defensive Programming Techniques
- Writing Highly Maintainable Unit Tests
- Improving Testability Through Design
Articles
- Here is Why Calling a Virtual Function from the Constructor is a Bad Idea
- What Makes List<T> So Efficient in .NET?
- Nondestructive Mutation and Records in C#
- Understanding Covariance and Contravariance of Generic Types in C#
- Using Record Types in C#
- Unit Testing Case Study: Calculating Median
- More...