Finding a Majority Element in an Array

by Zoran Horvat
May 18, 2013

Problem Statement

Given a large array of non-negative integer numbers, write a function which determines whether or not there is a number that appears in the array more times than all other numbers combined. If such element exists, function should return its value; otherwise, it should return a negative value to indicate that there is no majority element in the array.

Example: Suppose that array consists of values 2, 6, 1, 2, 2, 4, 7, 2, 2, 2, 1, 2. Majority element in this array is number 2, which appears seven times while all other values combined occupy five places in the array.

Keywords: Array, searching, majority, vote.

Problem Analysis

This problem can be viewed as the task of counting votes, where number of candidates is not determined in advance. Goal is to see if any of the candidates has collected more than half of all votes.

We could approach the problem in several ways. For example, we could sort the array and then simply count how many times each candidate appears. Since all occurrences of one value in sorted sequence are consecutive, determining the winner would be very simple. Here is the pseudo-code:

function FindMajoritySort(a, n)
a - unsorted integer array
n - number of elements in the array
begin

    SortArray(a, n) -- use external function for sorting

    winner = -1
    winCount = 0

    curCount = 0

    for i = 0, n - 1
        begin
            if a[i] = cur then
                curCount = curCount + 1
            else if curCount > winCount then
                winner = a[i - 1]
                winCount = curCount
                curCount = 1
            else
            curCount = 1
        end

    if curCount > winCount
        begin
            winner = a[n - 1]
            winCount = curCount
        end

    if winCount <= n - winCount then
        winner = -1

    return winner

end

This function is very efficient once the array is sorted. However, sorting the array takes time - O(NlogN) in general - and that will be the overall time complexity of this solution.

We might tackle the time complexity problem by somehow indexing the values while traversing the array. As long as data structure used to keep the counters runs in less than O(logN) time per read or write operation, we will be fine. And really, there is such a structure: hash table takes O(1) time to store a value or to find it. Here is the pseudo-code of the solution which relies on hash table to count how many times each element occurs in the array:

function FindMajorityHash(a, n)
a - unsorted integer array
n - number of elements in the array
begin

    hashtable -- used to index counts for each value

    winner = -1

    for i = 0, n - 1
        begin

            count = 1
            if hashtable.Contains(a[i]) then
                count = hashtable(a[i]) + 1

            hashtable(a[i]) = count

            if winner < 0 or count > hashtable(winner) then
                winner = a[i]

        end

    if 2 * hashtable(winner) <= n then
        winner = -1

    return winner

end

This function runs in O(N) time, but suffers a problem of a different sort. It requires additional space for the hash table, which is proportional to N. For a very large array, this may be a serious obstacle.

By this point we have devised one solution which runs in O(NlogN) time and O(1) space; another solution runs in O(N) time and O(N) space. Neither of the two is really good. It would be beneficial if we could devise a solution that takes good parts of both, i.e. a solution that runs in constant space and completes in time that is proportional to length of the array. We will try to construct a solution that runs in O(N) time and O(1) space.

First thing to observe when looking for a solution is that it requires one specific piece of information that survives during iteration through the array: counter that keeps track how many times one value occurs compared to all other values. Suppose that we know that there is a majority element and even that we know its value (call it M). We could run through the array and let that number outperform all other numbers. For instance, whenever we encounter value M in the array, we would increment some counter. On any other value, we would decrement the counter. Current value stored in the counter is the information which survives during the array traversal. It would go up and down, or might even be negative sometimes. But when end of the array is reached, value in the counter will definitely be positive because there was more increment than decrement operations. Figure below shows an example in which we are proving that number 1 is the majority value in an array.

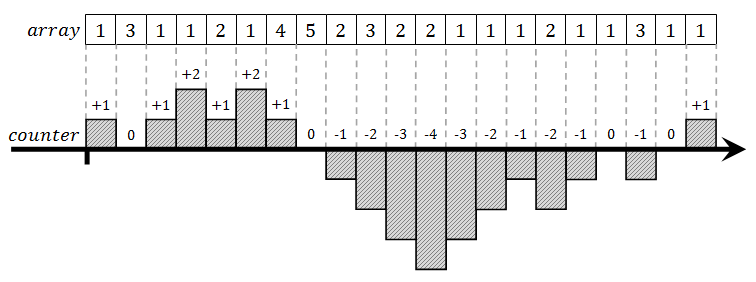
This idea does not solve the problem because we do not know the majority value in the first place. We could forget that value and pick any value (e.g. the first element of the array) as the majority candidate. As long as the count associated with this element is non-negative, we are fine: that element remains the good candidate. But what happens if count goes into negative values? Should end of the array occur at that particular place, then we would be in trouble because first element of the array is certainly not the one providing more than a half of the array population.

By this point we have identified the critical moment when counter becomes negative, i.e. moves from zero to -1, in which something must be done. One thing that we can do is to forget the majority candidate we had. But what if that really is the majority element, i.e. what if it catches up later and then goes into positive count again? The answer is simple. If it was in minority in the first part of the array, then it will have to be in even greater majority in the remainder of the array to compensate. So we're still fine even if we forget that value at the moment and switch to the new candidate, because we can reasonably expect the old candidate to beat the new one later and to become the majority candidate again. Now, which number is going to be the next candidate? One obvious solution is the current element, the one which has switched the count into negative range. That is convenient simply because we already have access to it. The same logic was applied when the first candidate was selected.

When this modified solution is applied to the whole array, we end up with a number which is the last majority candidate. We are still not sure whether this number is overall majority element of the array or not. But the selection process adds some qualities to that candidate. Let's observe the previous array when processed by this new algorithm.

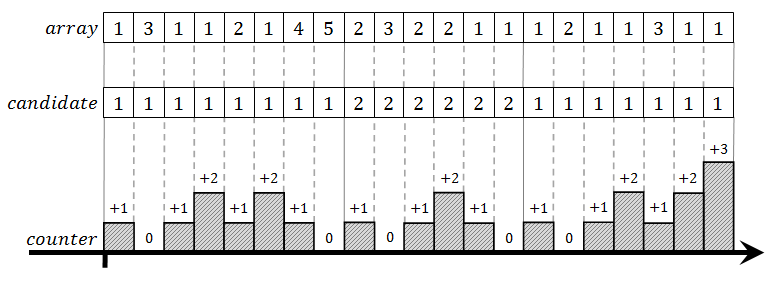
This time counter never goes into negative. It always bounces off the zero value and turns back into positive range, at the same time switching to the new majority candidate. The whole process now divides the array into segments. In each segment one number occurs as many times as all other numbers combined. In the worst case, those "all other numbers" will actually be a single number which occurs as many times as the candidate for that segment - we don't know whether that is the case or not, because we are counting only the candidate’s occurrences.

Anyway, when all segments align, the last segment alone decides the battle, and here is why. All segments except the last one look the same. First number in the segment is the special element and it occurs as many times as all other numbers in the segment combined. We know this fact because every segment ends with counter equal to zero (this is what candidate selection process guarantees). So all segments but the last one together are guaranteed not to contain a majority element. At best, there will be one number that occurs as many times as all the others combined, but not more than that. The only number that really could be the majority element of the array is the winner of the last segment, i.e. final majority candidate that remains when end of array is reached.

Now only the final touch remains. If last majority candidate has count greater than zero, then we should iterate through the array once again to test whether this value really occupies more than half of all positions in the array.

This complete solution requires a couple of variables to store current candidate and the counter. It passes the array once or twice. In the first pass, majority candidate is established. In the second pass we simply check whether the candidate is a solution or there is no majority element. This means that algorithm described runs in O(N) time and O(1) space.

Implementation will consist of two functions. First one will count occurrences of a number, subtracting other elements from the count. Majority element will be the value for which this function returns positive result. Another function will establish the majority candidate and then call the first function to decide whether it is the majority element or there is no majority element in the array. Here is the pseudo-code:

function GetCountForValue(a, n, x)
a - array of non-negative integers
n - number of elements in the array
x - number for which count is required
begin

    count = 0

    for i = 0, n-1
        begin
            if a[i] = x then
                count = count + 1
            else
                count = count - 1
        end

    return count

end

function FindMajorityElement(a, n)
a - array of non-negative integers
n - number of elements in the array
begin

    count = 1
    candidate = a[0]

    for i = 1, n-1
        begin

            if a[i] = candidate then
                count = count + 1
            else if count = 0 then
                candidate = a[i]
                count = 1
            else
                count = count – 1

        end

    if count > 0 then
        count = GetCountForValue(a, n, candidate)

    if count > 0 then
        return candidate

    return -1 -- there is no majority element

end

Implementation

Below are functions GetCountForValue and FindMajorityElement, coded in C#. The code is relatively simple, once all the analysis has been provided.

static int GetCountForValue(int[] a, int x)
{

    int count = 0;

    for (int i = 0; i < a.Length; i++)
        if (a[i] == x)
            count++;
        else
            count--;

    return count;

}


static int FindMajorityElement(int[] a)
{

    int count = 1;
    int candidate = a[0];

    for (int i = 1; i < a.Length; i++)
    {
        if (a[i] == candidate)
        {
            count++;
        }
        else if (count == 0)
        {
            candidate = a[i];
            count = 1;
        }
        else
        {
            count--;
        }
    }

    if (count > 0)
        count = GetCountForValue(a, candidate);

    if (count > 0)
        return candidate;

    return -1;

}

Demonstration

In this section we will provide functions that can generate a random array which sometimes has a majority element and sometimes not. Array is first populated by numbers 1, 2, 3, ... and then shuffled using the algorithm from Card Shuffling exercise . Once the array is generated, function FindMajorityElement is called to find the majority element. Here is the complete source code of the console application which demonstrates how FindMajorityElement function works:

using System;

namespace MajorityElement
{

    public class Program
    {

        static Random _rnd = new Random();

        static void RandomizeArray(int[] a)
        {

            for (int i = a.Length - 1; i > 0; i--)
            {
                int pos = _rnd.Next(i + 1);
                int x = a[pos];
                a[pos] = a[i];
                a[i] = x;
            }

        }

        static int[] GenerateArray(int n)
        {

            int value = 1;
            int pos = 0;
            int[] a = new int[n];

            while (pos < n)
            {
                int count = _rnd.Next(n - pos) + 1;
                while (count-- > 0)
                    a[pos++] = value;
                value++;
            }

            RandomizeArray(a);

            return a;

        }

        static void PrintArray(int[] a)
        {
            for (int i = 0; i < a.Length; i++)
                Console.Write("{0,3}", a[i]);
            Console.WriteLine();
        }

        static int GetCountForValue(int[] a, int x) { ... }

        static int FindMajorityElement(int[] a) { ... }

        public static void Main(string[] args)
        {

            while (true)
            {

                Console.Write("n=");
                int n = int.Parse(Console.ReadLine());

                if (n <= 0)
                    break;

                int[] a = GenerateArray(n);

                PrintArray(a);

                int majority = FindMajorityElement(a);

                if (majority < 0)
                    Console.WriteLine("No majority element.");
                else
                {
                    int count = 0;
                    for (int i = 0; i < n; i++)
                        if (a[i] == majority)
                            count++;
                    Console.WriteLine("Majority number is {0} (occurring {1} times).", majority, count);
                }
            }

            Console.Write("Press ENTER to continue... ");
            Console.ReadLine();

       }
    }

}

When application is run, it produces output like this:

            
n=10
  1  1  1  1  1  1  3  2  1  3
Majority number is 1 (occurring 7 times).
n=10
  3  4  1  1  3  2  1  1  4  1
No majority element.
n=10
  1  1  2  2  1  2  3  2  1  2
No majority element.
n=10
  1  2  1  1  1  1  3  1  1  1
Majority number is 1 (occurring 8 times).
  2  2  2  2  2  2  1  1  1  1
Majority number is 2 (occurring 6 times).
n=10
  2  2  4  1  1  1  3  1  1  3
No majority element.
n=0
Press ENTER to continue...
                
    

Follow-Up Exercises

Finding a majority element should not really be a problem. It almost looks like one could pick up a few elements at random and already have a majority element at hand. Off course, this is not exactly true, but it might be a good initial step towards the solution. We strongly recommend readers to try to devise a different method of finding the majority element in the array.

One idea might be to use partitioning algorithm from QUICKSORT algorithm.

Enhancement could be to find Kth smallest element using an efficient algorithm from Finding Kth Smallest Element in an Unsorted Array exercise. By picking up a single value for K smartly, we could find majority element in one attempt. Try to solve the problem starting from this idea.

---