Converting Number Bases

by Zoran Horvat
November 03, 2013

Problem Statement

Given a string representing a number, base in which the number is written and new base to which number should be converted, write a function which produces a string representing the same number in new base. Digits higher than 9 should be represented by capital letters A, B, ..., Z. Together with decimal digits 0 to 9, this makes total of 36 digits that can be represented. Hence, both bases will be numbers between 2 and 36, inclusive.

Example: For number 1002 with base 3 and new base 8 (octal number) output value should be 35. Same number in new base 10 would produce output 29, and in new base 16 (hexadecimal number) it would produce output 1D.

Problem Analysis

This exercise deals with numbers written in positional system. This means that each position is associated with specific "weight", or a multiplier applied to the digit at that position. Take decimal numeric system as an example. Weights associated with positions are one, for lowest digit, ten, for the following digit, a hundred, a thousand, and so on.

In general case, when number is written in positional system with base b with total of n digits, weights of positions would grow exponentially with position number: b^0, b^1, b^2, ... , b^n-1. Actual value of the number, given the values of its digits, is then:

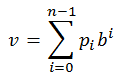
Now we can begin solving the problem. We are given a number in base b in form of a stream of digits. The task is to entail digits of another number in base d, so that values of two numbers are equal:

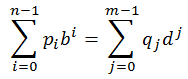
There are some oddities to note about this formula. First, bases of two numbers are different. Second thing is the consequence: number of digits differs in two numbers, in general case. Even more, although number of digits in the left-hand number (n) is known in advance, the length of the number on the right (m) is unknown. It could be deduced from n and number bases but, as will soon become obvious, we don't really need to know m.

It would be quite difficult to guess all the digits in the second number at once, given the number value (sum on the left side of the equation) and the target base d. This conclusion leads to the idea of entailing target number digits in some sort of an iterative process. One possibility is to build on the fact that lowest digit in the target number is solely determined by the overall number value. It is not affected by higher digits in any way (this is the core quality of all positional number systems). If we divide the left-hand sum by the base d, division remainder will be the value of lowest digit in the number on the right:

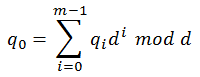
Now that we have decided the value of lowest digit, we can completely remove it from both sides of the equation:

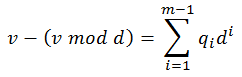
Even more, both sides of the equation are now divisible by d after remainder has been subtracted from them:

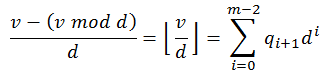
Net result of this transformation is that now we have got a completely new number in base b on the left side. At the same time, number on the right side in base d has all digits left intact, with only the lowest digit missing - the lowest digit has been eliminated from the equation. What used to be the second lowest digit in the target number has now become the least significant digit in the new target number.

Way forward from this point is quite simple. Just repeat the process once more to extract the next lowest digit in the target number. And again, repeat the process to calculate the next digit and so on. Digits are deduced one at a time, until all m digits are calculated. The only difficulty is that m is not known. So we need a stopping condition.

If we observe the process described above, we will notice that the number on the left side of the equation is reduced in every step. This comes from dividing that number with base d. As the process continues, we can expect that at some point the whole number is going to become equal to zero. Th would be the point in which we stop looking for more digits on the right. Should we continue, all further digits would be zero - leading zeros, in fact - and they are not needed.

So the stopping criterion is to look when the source number drops to zero. This comes with a trap: the source number might already be zero at the beginning, even before we have extracted the first digit for the resulting number in base d. In that case, the resulting number should also be set to zero and the whole calculation skipped entirely.

The core function which converts number bases is now fairly simple, although dependant on a couple of helper functions:

function ConvertNumber(number, b, d)
begin
    newNumber = ""
    while number <> "0"
        begin
            number = Divide(number, b, d, out remainder)
            newDigit = ValueToDigit(remainder)
            newNumber = Concatenate(newDigit, newNumber)
        end
    if newNumber ="" then
        newNumber = "0"
end

Most important helper function used is called Divide. It receives a number, its base and a divisor. On output, this function returns result of the division, which is a number in base which was specified as an argument. In addition, the function returns division remainder through an output parameter. Here is the pseudocode of this function:

function Divide(number, base, divisor, out remainder)
begin
    remainder = 0
    result = ""
    for i = 0 to Length(number) - 1
        begin
            digitValue = DigitToValue(number[i])
            remainder = base * remainder + digitValue
            newDigitValue = remainder / divisor -- integer division
            remainder = remainder mod divisor
            if newDigitValue > 0 OR result <> "" then
                newDigit = ValueToDigit(newDigitValue)
                result = Concatenate(result, newDigit)
        end
    if result = "" then
        result = "0"
    return result
end

There are a few points to mention in this function. First of all, implementation is based on simple pencil-and-paper algorithm. But the catch is that division is performed in specified base, rather than in decimal number system. As a consequence, we only have current digit and current remainder converted to integers at any given time. This is simply because division and modulo operations in programming languages are defined for integers, rather than for numbers with arbitrary base.

Nevertheless, this pencil-and-paper process produces one output digit in every step, and these digits are appended to the resulting number from most significant position towards less significant ones. And again, there is a catch. If digit produced on the output is zero and resulting number is empty (this is the first digit), then the digit is dropped. It would be a leading zero anyway, and it serves no purpose in the number apart from needlessly growing it in length. But then, there is another catch: if no digits are appended to the result by the end of the loop, then one zero is still passed to it (this is the result of the final if statement in the function). This step resolves the situation where all digits in the result are leading zeros, meaning that the whole output number is zero.

Implementation

Below is the complete implementation of console application in C# which converts number bases.

using System;

namespace ChangingBases
{

    public class OperationResult
    {

        static int DigitToValue(char digit)
        {

            int value = 0;

            if (digit >= '0' && digit <= '9')
                value = digit - '0';
            else // digit is between 'A' and 'Z'
                value = digit - 'A' + 10;

            return value;

        }

        static char ValueToDigit(int value)
        {

            char digit = '\0';

            if (value < 10)
                digit = (char)('0' + value);
            else
                digit = (char)('A' + (value - 10));

            return digit;

        }

        static string Divide(string number, int numberBase, int divisor,
                             out int remainder)
        {

            remainder = 0;
            string result = string.Empty;

            for (int i = 0; i < number.Length ; i++)
            {

                int digitValue = DigitToValue(number[i]);
                remainder = numberBase * remainder + digitValue;
                int newDigitValue = remainder  divisor;
                remainder = remainder % divisor;

                if (newDigitValue > 0 || result != string.Empty)
                {
                    char newDigit = ValueToDigit(newDigitValue);
                    result = result + newDigit;
                }

            }

            if (result == string.Empty)
                result = "0";

            return result;

        }

        static string ConvertNumber(string number, int numberBase,
                                    int newBase)
        {

            string newNumber = string.Empty;

            while (number != "0")
            {
                int reminder = 0;
                number = Divide(number, numberBase, newBase, out reminder);
                char newDigit = ValueToDigit(reminder);
                newNumber = newDigit + newNumber;
            }

            if (newNumber == string.Empty)
                newNumber = "0";

            return newNumber;

        }

        static void Main(string[] args)
        {

            Console.Write("Enter number (empty to exit): ");
            string number = Console.ReadLine();

            while (!string.IsNullOrEmpty(number))
            {

                Console.Write("    Enter number base (2-36): ");
                int numberBase = int.Parse(Console.ReadLine());

                Console.Write("Enter new number base (2-36): ");
                int newBase = int.Parse(Console.ReadLine());

                string newNumber = ConvertNumber(number, numberBase, newBase);

                Console.WriteLine("{0} ({1}) = {2} ({3})",
                                  number, numberBase, newNumber, newBase);

                Console.Write("Enter number (empty to exit): ");
                number = Console.ReadLine();

            }

        }

    }
}

Demonstration

When application is run, it produces output like this:

            
Enter number (empty to exit): 1002
    Enter number base (2-36): 3
Enter new number base (2-36): 8
1002 (3) = 35 (8)
Enter number (empty to exit): 1002
    Enter number base (2-36): 3
Enter new number base (2-36): 10
1002 (3) = 29 (10)
Enter number (empty to exit): 1002
    Enter number base (2-36): 3
Enter new number base (2-36): 16
1002 (3) = 1D (16)
Enter number (empty to exit): 97ADSFKH32497GH2
    Enter number base (2-36): 32
Enter new number base (2-36): 10
97ADSFKH32497GH2 (32) = 348659477389970058232354 (10)
Enter number (empty to exit):
                
    

---