Finding Mode of an Array

by Zoran Horvat
September 12, 2013

Problem Statement

Given an unsorted array of integer numbers, write a function which returns the number that appears more times in the array than any other number (mode of the array). If there are multiple solutions, i.e. two or more most frequent numbers occur equally many times, function should return any of them.

Example: Let the array be 1, 2, 2, 3, 1, 3, 2. Mode of this array is 2, and the function should return value 2. Should an additional value 1 appear in the array, so that it becomes 1, 2, 2, 3, 1, 3, 2, 1, the function should return either 2 or 1, because these are the numbers with most appearances - three times each.

Keywords: Array mode, mode of the array, relative majority, plurality, array.

Problem Analysis

In this exercise we are dealing with simple majority, meaning that the winning element is not required to populate more than half of the array. It is sufficient for the winner to just appear more often than the second most frequent element. This is a different requirement compared to the Majority Element exercise .

But this loose requirement actually makes the problem harder to solve. In case of proper (absolute) majority element, it is sufficient to find the median of the array and that element would either be the majority element, or the array would not contain the majority element at all. There is even simpler and more efficient algorithm for finding majority element, which is covered in exercise Finding a Majority Element in an Array .

With array mode, the difficulty comes from the fact that many numbers can share the winning position. Suppose that we try to count occurrences of each number in the array in order to find which one occurs more times than others. In the worst case, all numbers could be distinct, and then all of them would share the same place with exactly one occurrence.

Of course, that would mean that there is no single winner, but that conclusion can only be made after the very last element of the array has been visited. Suppose that the last number in the array is not unique, but instead is a repetition of one of the preceding elements. In that case, that particular number would be the winner with total of two occurrences - just enough to beat all other competing elements by one.

Indexing Solution

Following the analysis, the first solution could be to just count occurrences of each distinct element in the array. We could use the hash table data structure, which has O(1) search time. Hash table would be used to map element value to total number of occurrences of that value.

Whenever an element of the array is visited, we search for that value in the hash table. If the value is there, then it maps to total number of occurrences of that value in the array so far. Therefore, we just increment the count in the hash table and move forward. Otherwise, if this is the first occurrence of the value in the array, we just add it to the hash table with associated count equal to one.

Here is the pseudocode of the counting solution:

function Mode(a, n)
    a - array of integers
    n - length of the array
begin
    index = new hashtable
    mode = 0
    modeCount = 0
    for i = 1 to n
        begin

            if index contains a[i] then
                begin
                    index[a[i]] = index[a[i]] + 1
                    curCount = index[a[i]]
                end
            else
                begin
                    index[a[i]] = 1
                    curCount = 1
                end

            if curCount > modeCount then
                begin
                    mode = a[i]
                    modeCount = curCount
            end

            return mode

        end
end

This function takes only O(1) time to calculate the array mode, provided that the hash table it uses exhibits O(1) access time. But on the other hand, this function takes O(N) memory to build the index of all distinct elements in the array. In the worst case, when all elements are distinct, index size will be proportional to the array size.

Counting Sort Solution

In some cases we could simplify the indexing solution. If we knew that the range of numbers appearing in the array is bounded to a reasonable range, then we could apply the counting sort algorithm and just count occurrences of each value in the array.

Here is the pseudocode of the function which calculates the array mode by counting:

function Mode(a, n)
    a - array of integers
    n - length of the array
begin
    min = minimum value in a
    max = maximum value in a
    range = max - min + 1

    counters = new int array [0..range - 1]
    for i = 0 to range - 1
        counters[i] = 0

    for i = 1 to n
        begin
            offset = a[i] - min
            counters[offset]  = counters[offset] + 1
     end

    modeOffset = 0

    for i = 1 to range - 1
        if counters[i] > counters[modeOffset] then
            modeOffset = i

     mode = min + modeOffset

    return mode

end

This function takes O(N) time to count occurrences in the array. It also takes O(range) to initialize the counters and then again O(range) to find the maximum counter. Overall time complexity is O(N) + O(range), while space required to keep the counters is O(range).

From asymptotic complexity we can easily conclude that this solution is applicable when range of values in the array does not exceed the array size - range = O(N). In that case the function would require O(N) time and O(N) space to execute.

Now that we have two solutions based on counting array elements, we could ask whether there is another way to solve this problem without taking additional space outside the array? That will be the goal of the next solution that we will present.

Quicksort Solution

We could easily find the array mode by first sorting the array and then counting successive elements that are equal. The sorting step would take O(NlogN) time to complete. The subsequent counting step would take O(N) time to find the most frequent element.

On the other hand, no additional memory would be required, because both sorting and counting take O(1) space. This is the compromise compared to previous solution. We are spending somewhat more time, but we are preserving memory.

Here is the pseudocode of the function which relies on external sorting algorithm:

function Mode(a, n)
    a – array of integers
    n – length of the array
begin

    sort a -- use algorithm with O(NlogN) time

    mode = 0
    modeCount = 0

    curValue = 0
    curCount = 0

    for i = 1 to n
        begin
            if a[i] = curValue then
                begin
                    curCount = curCount + 1
                end
            else
                begin

                   if curCount > modeCount then
                       begin
                           mode = curValue
                           modeCount = curCount
                       end

                    curValue = a[i]
                    curCount = 1

                end
        end

    if curCount > modeCount
        mode = curValue

    return mode

end

Counting loop in this function is a little bit complicated. At every step, we are keeping record of the previous value in the array, as well as total number of its appearances so far. If current array element is the same as the previous one, then we just increase the counter. Otherwise, we have reached the end of counting for the previous value. In that case we have to test whether the better candidate has been found and to reset the counter for the next value in the array. Of course, when the all the elements are exhausted, the last one can still be the best one. We have to test whether it has beaten the previously most frequent element.

This solution looks like a step in the right direction, but we can also come to a better solution. Do we have to sort the array completely? Probably not – sections of the array that are shorter than the best candidate this far can freely be left unsorted. That idea will be discussed in the next section.

Partial Sorting Solution

One possible improvement on the sorting solution would be to partition the array in a way similar to what Quicksort does. Just pick up an element (pivot) and divide the array by comparing all elements against the pivot. Elements that are strictly less than the pivot will go to the beginning of the array. Elements strictly greater than the pivot will be moved to the end of the array. And in between shall we put all the elements equal to the pivot.

In this way we have made one step forward in search for the mode. Namely, we have isolated one element of the array (the pivot from previous step) and found total number of its occurrences in the whole array. Now we apply the process recursively, first to the left partition of the array, and then to the right partition. But not the same in all cases. There are circumstances under which it makes no sense to process certain partition further because it cannot provide a candidate better than the one found so far.

Any partition is processed recursively only if it is larger than the count of the best candidate found this far. Otherwise there would be no point in spending time to count elements of the partition because none of them could ever beat the same frequency as the current candidate.

Here is the pseudocode of the mode function which partially sorts the array:

function Mode(a, n)
    a – array of integers
    n – length of the array
begin

    mode = 0
    modeCount = 0

    ModeRecursive(a, 1, n, in/out mode, in/out modeCount);

    return mode

end

function ModeRecursive(a, lower, upper, in/out mode, in/out modeCount)
    a – array of integers
    lower – lower inclusive index of the array that should be processed
    upper – upper exclusive index of the array that should be processed
    mode – on input current best candidate; on output new best candidate
    modeCount – on count of the current best candidate
begin

    pivot = array[begin] -- We could use a better algorithm

    left = lower
    right = upper - 1

    pos = left;
    while (pos <= right)
        begin
            if array[pos] < pivot
                begin
                    array[left++] = array[pos]
                    pos = pos + 1
                end
            else if array[pos] > pivot
                begin
                    swap array[right] and array[pos]
                    right = right – 1
                end
            else
                begin
                    pos = pos + 1
                end
        end

    pivotCount = right - left + 1

    for i = left to right
        array[i] = pivot

    if pivotCount > mode.Count
        begin
            mode.Value = pivot;
            mode.Count = pivotCount;
        end

    leftCount = left - begin
    if leftCount > mode.Count
        mode = FindModePartialSortRecursive(array, begin, left, mode)

    rightCount = end - right - 1
    if rightCount > mode.Count
        mode = FindModePartialSortRecursive(array, right + 1, end, mode)

    return mode

end

Recursive function is the one which does all the work. It first partitions the array and counts the pivot occurrences. Should the pivot be more frequent than the previously discovered mode candidate, the pivot becomes new candidate.

After this step, operation is recursively performed on left and right partition. Observe that both partitions are excluding the pivot in this solution. This lets us include the optimization. We do not process a partition unless it is longer than number of occurrences of the current mode candidate. Once again, this is because such partition could not contain any candidate better than the one we already have.

Finally, when recursion unfolds, candidate it returns is the overall best element, which is the mode of the array.

Non-recursive function at the beginning only delegates the call to the recursive implementation and then returns its overall result.

Implementation

Below is the full implementation of a console application in C# which allows user to select size of a randomly generated array. Application then searches for the simple majority element in the array and prints its value on the console.

Although only the partial sort function is called in this solution, you can find all four mode functions in the code.

using System;
using System.Collections.Generic;

namespace ArrayMode
{

    struct Mode
    {
        public int Value;
        public int Count;
    }

    class Program
    {

        static void Print(int[] a)
        {

            for (int i = 0; i < a.Length; i++)
            {
                Console.Write("{0,3}", a[i]);
                if (i < a.Length - 1 && (i + 1) % 10 == 0)
                    Console.WriteLine();
            }
            Console.WriteLine();
            Console.WriteLine();

            Array.Sort(a);
            int count = 0;
            for (int i = 0; i < a.Length; i++)
            {
                if (i == 0)
                    count = 1;
                else if (a[i] == a[i - 1])
                    count++;
                else
                {
                    Console.WriteLine("{0,3} x {1}",
                                      a[i - 1], count);
                    count = 1;
                }
            }

            Console.WriteLine("{0,3} x {1}",
                              a[a.Length - 1], count);

        }

        static Mode FindModeHash(int[] array)
        {

            Mode best = new Mode();
            Dictionary<int, int> hashtable =
                new Dictionary<int, int>();

            foreach (int value in array)
            {
                int curCount;
                int count = 1;
                if (hashtable.TryGetValue(value, out curCount))
                    count = curCount + 1;

                hashtable[value] = count;

                if (count > best.Count)
                {
                    best.Value = value;
                    best.Count = count;
                }
            }

            return best;

        }

        static Mode FindModeCountingSort(int[] array)
        {

            int min = array[0];
            int max = array[0];

            for (int i = 1; i < array.Length; i++)
            {
                if (array[i] < min)
                    min = array[i];
                if (array[i] > max)
                    max = array[i];
            }

            int range = max - min + 1;

            // All elements automatically reset to 0
            int[] counters = new int[range];

            for (int i = 0; i < array.Length; i++)
            {
                int offset = array[i] - min;
                counters[offset]++;
            }

            int modeOffset = 0;

            for (int i = 1; i < range; i++)
                if (counters[i] > counters[modeOffset])
                    modeOffset = i;

            Mode mode = new Mode()
            {
                Value = min + modeOffset,
                Count = counters[modeOffset]
            };

            return mode;

        }

        static Mode FindModeSort(int[] array)
        {

            Array.Sort(array);

            Mode current = new Mode()
            {
                Value = array[0],
                Count = 1
            };

            Mode best = new Mode();

            for (int i = 1; i < array.Length; i++)
            {
                if (array[i] != current.Value)
                {

                    if (current.Count > best.Count)
                        best = current;

                    current.Value = array[i];
                    current.Count = 1;

                }
                else
                {
                    current.Count++;
                }
            }

            if (current.Count > best.Count)
                best = current;

            return best;

        }

        static Mode FindModePartialSort(int[] array)
        {
            return FindModePartialSortRecursive(array, 0, array.Length,
                                                new Mode());
        }

        static Mode FindModePartialSortRecursive(int[] array, int begin,
                                                 int end, Mode best)
        {

            Mode mode = best;
            int pivot = array[begin]; // Use better pivot selection

            int left = begin;
            int right = end - 1;

            int pos = left;
            while (pos <= right)
            {
                if (array[pos] < pivot)
                {
                    array[left++] = array[pos];
                    pos++;
                }
                else if (array[pos] > pivot)
                {
                    int tmp = array[right];
                    array[right--] = array[pos];
                    array[pos] = tmp;
                }
                else
                {
                    pos++;
                }
            }

            int pivotCount = right - left + 1;

            for (int i = left; i <= right; i++)
            {
                array[i] = pivot;
            }

            if (pivotCount > mode.Count)
            {
                mode.Value = pivot;
                mode.Count = pivotCount;
            }

            int leftCount = left - begin;
            if (leftCount > mode.Count)
            {
                mode = FindModePartialSortRecursive(array, begin,
                                                    left, mode);
            }

            int rightCount = end - right - 1;
            if (rightCount > mode.Count)
            {
                mode = FindModePartialSortRecursive(array, right + 1,
                                                    end, mode);
            }

            return mode;

        }

        static void Main(string[] args)
        {

            Random rnd = new Random();
            int n = 0;

            while (true)
            {

                Console.Write("Array length (0 to exit): ");
                n = int.Parse(Console.ReadLine());

                if (n <= 0)
                    break;

                int[] a = new int[n];
                for (int i = 0; i < a.Length; i++)
                    a[i] = rnd.Next(9) + 1;

                Print(a);

                Mode mode = FindModePartialSort(a);

                Console.WriteLine("Mode of the array is {0}; " +
                                  "it occurs {1} times.",
                                  mode.Value, mode.Count);

                Console.WriteLine();

            }

        }
    }
}

Demonstration

When application above is run, its output may look something like this:

            
Array length (0 to exit): 10
  6  7  1  1  8  5  4  6  4  4

  1 x 2
  4 x 3
  5 x 1
  6 x 2
  7 x 1
  8 x 1
Mode of the array is 4; it occurs 3 times.

Array length (0 to exit): 17
  3  3  6  9  8  1  6  5  8  9
  2  6  9  2  9  6  8

  1 x 1
  2 x 2
  3 x 2
  5 x 1
  6 x 4
  8 x 3
  9 x 4
Mode of the array is 6; it occurs 4 times.

Array length (0 to exit): 20
  7  4  2  2  5  7  9  4  5  9
  3  2  7  9  9  2  6  5  6  3

  2 x 4
  3 x 2
  4 x 2
  5 x 3
  6 x 2
  7 x 3
  9 x 4
Mode of the array is 2; it occurs 4 times.

Array length (0 to exit): 30
  9  8  8  6  2  6  2  2  6  2
  3  4  7  4  6  2  2  5  1  5
  3  2  1  5  3  1  8  1  6  4

  1 x 4
  2 x 7
  3 x 3
  4 x 3
  5 x 3
  6 x 5
  7 x 1
  8 x 3
  9 x 1
Mode of the array is 2; it occurs 7 times.

Array length (0 to exit): 50
  9  9  3  4  5  5  2  5  7  4
  8  9  1  8  5  2  2  7  3  8
  6  5  7  7  3  3  2  4  5  7
  6  9  6  8  3  8  8  3  7  5
  8  6  8  8  2  1  7  7  3  1

  1 x 3
  2 x 5
  3 x 7
  4 x 3
  5 x 7
  6 x 4
  7 x 8
  8 x 9
  9 x 4
Mode of the array is 8; it occurs 9 times.

Array length (0 to exit): 0
Press ENTER to continue...
                
    

Comparison of Methods

In this exercise we have seen four solutions to the same problem: hash table, counting sort, Quicksort and partial sorting. Each of the methods exhibits its own strengths and weaknesses. Graph below shows how much time each of the algorithms takes on an array with one million elements. Varying factor is total number of occurrences of the most frequent element in the array.

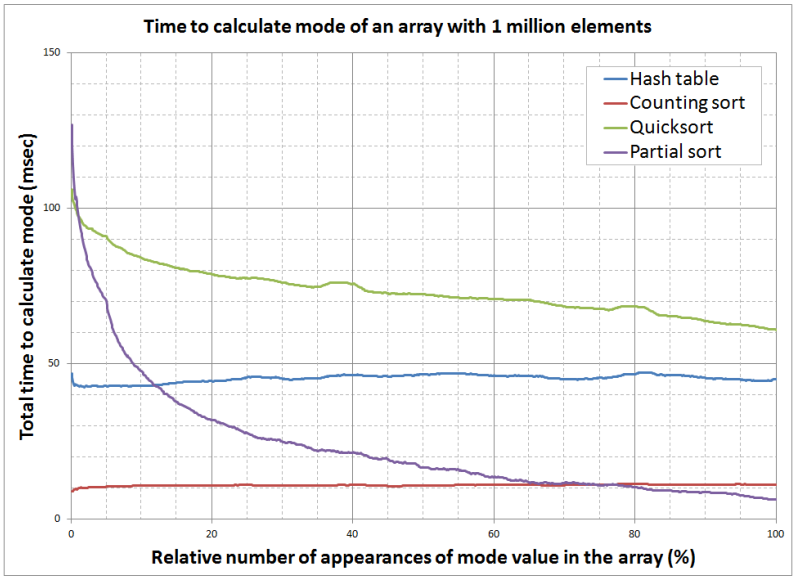
We can see that indexing methods are behaving quite differently from sorting methods. Hash table and counting sort both exhibit constant performance regardless of the data. Sorting solutions gradually improve as total number of values in the array goes down. Quicksort solution is improving because it is somewhat easier to sort the array with many repeating elements. Partial sort solution, on the other hand, is exhibiting significantly better performance as the array becomes more uniform because then it can cut the recursion much higher in the call hierarchy. This further leads to significant savings in execution time.

To truly compare these four methods, we have to remember that hash table and counting sort require additional memory. Even more, counting sort requires the range from which numbers in the array are selected is quite limited. In the experiment from which the results are shown in the diagram, range of the values was smaller than the array length. Under such ideal circumstances, we should not be surprised that the counting sort method was by far better than any other.

The next well performing method is hash table, followed by custom algorithm based on partial application of the Quicksort algorithm. Worst performance was exhibited by the Quicksort algorithm. This is clearly because total sorting of the array is not really necessary to calculate the array mode, so this solution was working more than necessary.

Overall conclusion is that algorithm that we should pick depends on the situation:

• If data are selected from a limited range, and memory proportional to the range of the values is available, then counting sort is the algorithm of choice.
• If data are selected from an excessively large range, but memory proportional to size of the array is available, then indexing is the best option.
• If in-place algorithm is a hard requirement, then partial sort is definitely better choice than using the built-in Sort function.

This concludes the analysis of algorithms for finding the array mode.

---