Paginating an Unsorted Array
by Zoran Horvat
Problem Statement
Given an unsorted array containing N integer numbers, write a function which extracts one page from sorted version of the array. Page is a range of elements occupying positions M, M+1, M+2, ... , M+P-1 in the array, where M marks beginning of the page (0 <= M < N) and P is the page size (M+P-1 < N). Function should place elements belonging to the requested page to their dedicated locations, so that the requested page is sorted when function completes.
Example: Suppose that array consists of numbers 6, 2, 5, 7, 8, 3, 1, 4, 9. Pages consist of four elements each (except the last one) and we require second page (M=4, P=4). After modifying the array, numbers 5, 6, 7 and 8 should be located starting from position 4. For example, this array content is a legitimate solution: 9, 2, 1, 3, 5, 6, 7, 8, 4. Note that other values in the array are not relevant, as long as the second page is sorted and in place.
Keywords: Array, sorting, pagination.
Problem Analysis
This is obviously a sorting problem and it is trivially solved by sorting the whole array. In that case all elements will be in their proper places in the sorted order, and so will be the requested page. But this solution does more than it is asked for. It prepares all other pages as well, pages into which the caller is not really interested. Imagine an array containing millions of numbers and a call made to the function to sort only elements on positions 50-59, inclusive. This would be the sixth page, where each page contains ten elements. There is no point in sorting the remaining 999,990 numbers in the array. One might think that the caller is likely to call the function many times again, asking for all the other pages, so why not sorting the whole array immediately? The answer is that, when things come to large arrays, it often happens that the caller is interested only in a tiny fraction of data contained.
As an illustration, consider a problem of querying a search engine with a relatively general query. The engine might detect millions of Web pages that satisfy the query, but only the first couple of them (say, ten links) will be communicated back to the customer. When customer asks for the second page with results, only then will the search engine bother to sort the following ten links. It rarely happens that any Web user walks more than a couple of pages at length before finding the desired document (or modifying the search query). Sorting the whole result set would be a tremendous waste of resources on the server because user is eventually going to leave without looking into anything beyond the leading few pages.
The conclusion is that efficient function should focus only on the requested range of elements. Any operation that does not get us nearer to the goal of bounding that range should be avoided. One way to approach the problem is to modify the sorting algorithm so that it only partially sorts the array. Good candidate for this idea is the QUICKSORT algorithm. Its partitioning step could eliminate quite a lot of elements that fall below or above the requested page. The following picture shows how to extract the second page containing three elements from a somewhat longer array than the one in the previous example.
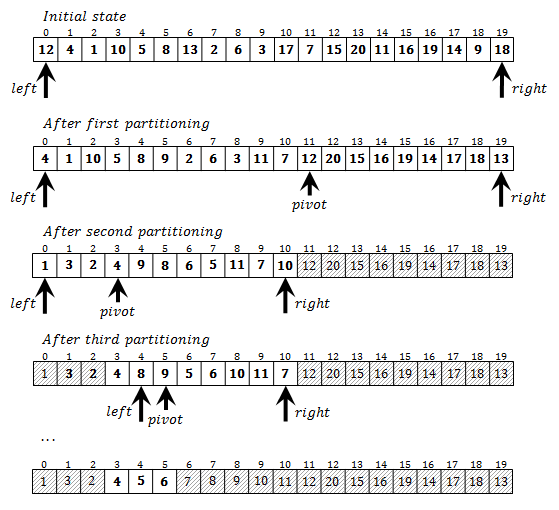
In this example we have not fully sorted the array. When deciding whether to sort elements that fall to one specific side from the pivot element (left or right), we check whether elements on that side overlap with requested positions 3, 4 and 5. If not, then there is no point in sorting that range of the array – such discarded elements are shaded gray in the figure above. As process continues, shaded parts of the array grow larger, until only the requested page remains for sorting. Some of the shaded elements are indeed sorted, but that is the pure coincidence. There is no intention to sort anything below or above the page.
This solution is efficient because it tends to identify elements that do not belong to the requested page and to discard them completely from further steps. Note that shaded parts of the array are not sorted at the end of the program execution. This is consequence of the fact that they are ignored by the algorithm.
Here is the pseudo-code which solves the pagination problem:
function Paginate(a, n, m, p)
a – unsorted array
n – number of elements in the array
m – position of the first element in the page
p – page size
begin
PaginateRecursive(a, 0, n – 1, m, p)
end
function PaginateRecursive(a, left, right, m, p)
a – unsorted array
left – position of the first element in current scope
right – position of the last element in current scope
m – position of the first element in the page
p – page size
begin
pivotPos = Partition(a, left, right) -- Partition function from QUICKSORT
-- Recursively paginate elements to the left of the pivot
-- if left-hand partition overlaps with requested page
-- These elements are located between left and pivotPos-1, inclusively
if (left < m + p AND pivotPos – 1 >= m AND pivotPos > left)
PaginateRecursive(a, left, pivotPos – 1, m, p)
-- Recursively paginate elements to the right of the pivot
-- if right-hand partition overlaps with requested page
-- These elements are located between pivotPos+1 and right, inclusively
if (pivotPos + 1 < m + p AND right >= m AND pivotPos < right)
PaginateRecursive(a, pivotPos + 1, right, m, p)
end
The main function is Paginate – it receives the array, its length and information about the page requested. But this function merely delegates the call to the recursive implementation (PaginateRecursive function), which in turn receives the bounds within the array which are currently in scope. This function relies on the Partition function from QUICKSORT algorithm, for which any implementation will suffice. For example, partitioning could be implemented like this:
function Partition(a, left, right)
a – unsorted array
left – index of the first element of the range to partition
right – index of the last element of the range to partition
begin
pivot = a[left]
pos = left + 1
while pos <= right
begin
if a[pos] < pivot then
begin
a[left] = a[pos]
left = left + 1
pos = pos + 1
end
else
begin
tmp = a[right]
a[right] = a[pos]
a[pos] = tmp
right = right - 1
end
end
a[left] = pivot
return left
end
In this implementation the first element in the range is picked up to be the pivot. After that, all elements that are strictly less than the pivot are moved towards the beginning of the range and all elements greater or equal to the pivot are moved towards the end of the range. Finally, pivot is placed in between and its new position is returned from the function.
Note that this implementation of the partitioning function is not very efficient. It may lead to high worst case running time in case when pivot falls to one or the end of the partitioned range. Readers are advised to provide the Partition function implementation with better pivot selection. Anyway, with this function in place, we are ready to provide the complete pagination solution.
Implementation
Below is implementation for the Paginate function and the two helper functions it relies on.
void Paginate(int[] a, int m, int p)
{
PaginateRecursive(a, 0, a.Length - 1, m, p);
}
void PaginateRecursive(int[] a, int left, int right, int m, int p)
{
int pivotPos = Partition(a, left, right);
if (left < m + p && pivotPos - 1 >= m && pivotPos > left)
PaginateRecursive(a, left, pivotPos - 1, m, p);
if (pivotPos + 1 < m + p && right >= m && pivotPos < right)
PaginateRecursive(a, pivotPos + 1, right, m, p);
}
int Partition(int[] a, int left, int right)
{
int pivot = a[left];
int pos = left + 1;
while (pos <= right)
{
if (a[pos] < pivot)
{
a[left++] = a[pos++];
}
else
{
int tmp = a[right];
a[right] = a[pos];
a[pos] = tmp;
right--;
}
}
a[left] = pivot;
return left;
}
Demonstration
In this section we are providing the complete source code of a console application which demonstrates using the Paginate function.
using System;
namespace Pagination
{
class Program
{
private static Random _rnd = new Random();
public static void ShuffleArray(int[] a)
{
for (int i = a.Length - 1; i > 0; i--)
{
int index = _rnd.Next(i + 1);
int tmp = a[i];
a[i] = a[index];
a[index] = tmp;
}
}
public static int[] GenerateArray(int n)
{
int[] a = new int[n];
for (int i = 0; i < n; i++)
a[i] = i + 1;
ShuffleArray(a);
return a;
}
public static void Paginate(int[] a, int m, int p) { ... }
public static void PaginateRecursive(int[] a, int left, int right,
int m, int p) { ... }
public static int Partition(int[] a, int left, int right) { ... }
public static void PrintArray(int[] a, int m, int p)
{
for (int i = 0; i < a.Length; i++)
Console.Write("{0}{1,2}{2}",
i == m ? "[" : " ",
a[i],
i == m + p - 1 ? "]" : " ");
if (m + p > a.Length)
Console.Write("]");
Console.WriteLine();
}
static void Main(string[] args)
{
while (true)
{
Console.Write("n=");
int n = int.Parse(Console.ReadLine());
if (n <= 0)
break;
Console.Write("m=");
int m = int.Parse(Console.ReadLine());
Console.Write("p=");
int p = int.Parse(Console.ReadLine());
int[] a = GenerateArray(n);
Paginate(a, m, p);
PrintArray(a, m, p);
}
Console.Write("Press ENTER to continue... ");
Console.ReadLine();
}
}
}
When application is run, it produces output like this:
n=10
m=3
p=3
1 3 2 [ 4 5 6] 7 8 10 9
n=15
m=8
p=4
4 3 2 1 5 6 7 8 [ 9 10 11 12] 13 15 14
n=20
m=3
p=3
1 3 2 [ 4 5 6] 7 8 9 10 11 12 20 15 16 19 14 17 18 13
n=0
Press ENTER to continue...
Follow-Up Exercises
Readers are advised to modify existing solution and implement a function which sorts next page in a sequence, assuming that all previous pages, i.e. pages with smaller starting positions, are already sorted. Write a function with this signature:
void PaginateNext(int[] a, int m, int p)
All elements of the array in range 0 to m-1 are already sorted. On output, function should ensure that all elements on positions 0 to m+p-1 are sorted.
If you wish to learn more, please watch my latest video courses

Beginning Object-oriented Programming with C#
In this course, you will learn the basic principles of object-oriented programming, and then learn how to apply those principles to construct an operational and correct code using the C# programming language and .NET.
As the course progresses, you will learn such programming concepts as objects, method resolution, polymorphism, object composition, class inheritance, object substitution, etc., but also the basic principles of object-oriented design and even project management, such as abstraction, dependency injection, open-closed principle, tell don't ask principle, the principles of agile software development and many more.
More...

Design Patterns in C# Made Simple
In this course, you will learn how design patterns can be applied to make code better: flexible, short, readable.
You will learn how to decide when and which pattern to apply by formally analyzing the need to flex around specific axis.
More...

Refactoring to Design Patterns
This course begins with examination of a realistic application, which is poorly factored and doesn't incorporate design patterns. It is nearly impossible to maintain and develop this application further, due to its poor structure and design.
As demonstration after demonstration will unfold, we will refactor this entire application, fitting many design patterns into place almost without effort. By the end of the course, you will know how code refactoring and design patterns can operate together, and help each other create great design.
More...

Mastering Iterative Object-oriented Development in C#
In four and a half hours of this course, you will learn how to control design of classes, design of complex algorithms, and how to recognize and implement data structures.
After completing this course, you will know how to develop a large and complex domain model, which you will be able to maintain and extend further. And, not to forget, the model you develop in this way will be correct and free of bugs.
More...
About

Zoran Horvat is the Principal Consultant at Coding Helmet, speaker and author of 100+ articles, and independent trainer on .NET technology stack. He can often be found speaking at conferences and user groups, promoting object-oriented and functional development style and clean coding practices and techniques that improve longevity of complex business applications.
Elsewhere
Video Courses
- Making Your C# Code More Object-oriented
- Beginning Object-oriented Programming with C#
- Collections and Generics in C#
- Design Patterns in C# Made Simple
- Refactoring to Design Patterns
- Mastering Iterative Object-oriented Programming in C#
- Making Your C# Code More Functional
- Making Your Java Code More Object-oriented
- Writing Purely Functional Code in C#
- Tactical Design Patterns in .NET: Creating Objects
- Tactical Design Patterns in .NET: Control Flow
- Tactical Design Patterns in .NET: Managing Responsibilities
- Advanced Defensive Programming Techniques
- Writing Highly Maintainable Unit Tests
- Improving Testability Through Design
Articles
- Here is Why Calling a Virtual Function from the Constructor is a Bad Idea
- What Makes List<T> So Efficient in .NET?
- Nondestructive Mutation and Records in C#
- Understanding Covariance and Contravariance of Generic Types in C#
- Using Record Types in C#
- Unit Testing Case Study: Calculating Median
- More...