Simple Arithmetic Expression Evaluator
by Zoran Horvat
Problem Statement
Given a string representing an expression which consists of non-negative round numbers and four basic arithmetic operations, write a function which calculates final value of the expression. Although only non-negative numbers are allowed, end result or intermediate results may be negative. Four operations are: +, -, * and / (integer division, i.e. remainder is ignored). Expression may contain parentheses. Assume that expression is syntactically correct: all operators have proper left and right operand, parentheses are properly nested and balanced.
Examples:
- 3+2 produces result 5.
- 4/3 produces result 1.
- 2*(3+6/2)/4 produces 3.
- 6-9 produces -3.
Keywords: Calculator, expression evaluator, arithmetic operations.
Problem Analysis
In order to calculate an arithmetic expression, we need to know precise order in which operators are executed. Operations are not always performed in the same order, and that is from where most of the troubles are coming. Consider these two expressions: 2+3+4 and 2+3*4.
In the first case, addition operators are executed as they appear, from left to right. In the second case, the order is opposite because multiplication takes precedence over addition. Off course, taking precedence can be prevented by placing parentheses: (2+3)*4.
Everything seems to be fine as long as there are only two operators involved. But observe a little bit more complex expression: 2*(3+6/2)/4. To solve expression of this level of complexity, we need better suited tools. One standard solution to the problem is to build an expression tree. Nodes in the tree are operations (signified by their operators) and branches lead to operands. Leaf nodes in the tree are plain values, and they do not require further evaluation. Here is the tree representing the last expression listed above:
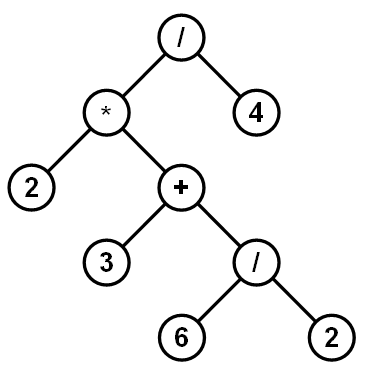
All inner nodes in this thee have exactly two child nodes each. This is simply because we were using binary operators only. Should the expression contain unary minus operator, it would contain a node with single child. Consider the following expression which utilizes unary minus: -(2+4)/3. And here is the corresponding expression tree:
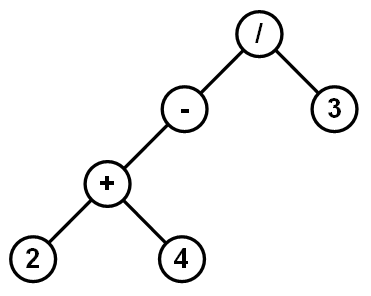
Now, in order to calculate the expression value, we need to execute all operations in the tree. Basically, when both child nodes contain plain values, node can be evaluated immediately. Otherwise, if at least one child node is an operator, then that operator must be evaluated first. Let’s see how this process goes on an example:
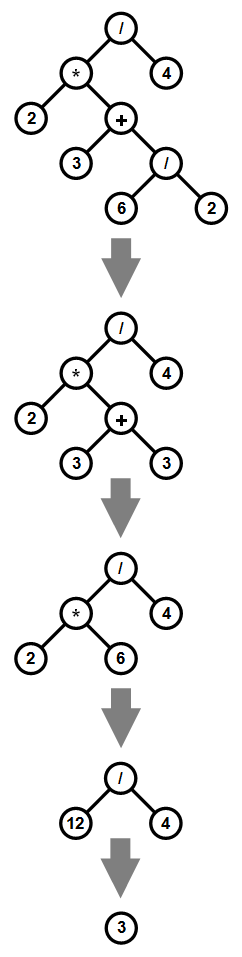
By reducing one node at the time, we gradually progress towards the tree root. Process ends when only the root node remains. Its value is then the overall result. The whole process could also be run recursively, starting from the root node. Node’s value is then determined like this:
- If node contains a number, then this number is node's value.
- Otherwise, i.e. node contains an operator, recursively obtain values of child nodes and execute the operation to determine the value.
Child nodes are called recursively, which in turn will trigger evaluation of their children and so on. Once all recursive calls unfold, root node's value will be in place.
Now the only problem remaining is how to turn an expression into corresponding expression tree. The process should be to iterate through the input string, which represents the expression, and to act upon each item encountered. Reading numbers is a straight-forward part of this task. Each number should simply be converted into a numeric node in the tree and that's where the processing ends. But problems begin when an operator is encountered. First of all, at the position of any binary operator, all we have at hand is the left operand and the operator sign. Right-hand operand is still waiting to be processed. On a completely different track, the last number read from the input might not be the left operand of a current operator! This is the consequence of operator precedence – current operator might have low precedence compared to last operator seen. Consider the following expression: 2+3+5. Items, in order of appearance, are:
- Number 2 – turns into a plain numeric node and it’s already processed.
- Operator + - still has no effect because right operand is yet to arrive.
- Number 3 – possibly a right operand for the + operator, but we still have to wait; for example, if this value is followed by the * operator, then number 3 would become the left operand for the multiplication operation, rather than the right operand for the addition.
- Operator + - another addition operator which now clears up the situation regarding the first + operator. Now that we know that this operator has the same precedence as the previous one, we could execute the previous operator and complete its processing. The first operator becomes a parent node and numbers 2 and 3 are its children. This whole structure will later be the left child for the second + operator.
- Number 5 – This number becomes the right operand for the second + operator.
Figure below demonstrates the process of building the tree for expression 2*(3+6/2)/4.
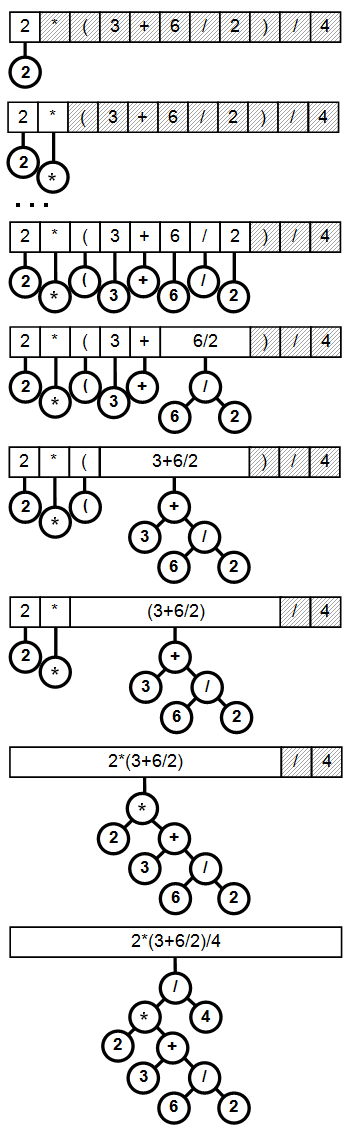
Calculation begins in a series of "do nothing" steps. None of the leading three operators can be executed as they appear. The first operator, multiplication, is isolated from the following addition operator by an open parenthesis. The addition operator itself has lower precedence compared to its follower, division operator, and waits for a better opportunity to evaluate its operands. The first real event occurs when closing parenthesis arrives. It causes all operators to unfold until the corresponding open parenthesis is reached. What remains after that point is another division operator. Since its predecessor is a multiplication operator, which has the same precedence, first to execute is multiplication and only then turn comes to the division. That is the complete sequence of events leading to construction of the final expression tree.
This comprehensive analysis of building an expression tree leads to a set of fairly simple conclusions. Decision whether to execute one operator or not is made upon the operator that follows it. Even better: each operator causes its preceding operator(s) to execute, but only if they had higher precedence. This will lead us to a sort of precedence table which may look as follows. The table shows whether or not the current operator causes preceding operator to evaluate, for all pairs of current and preceding operators.
| Current operator | Preceding operator | ||||
|---|---|---|---|---|---|
| + | - | * | / | ( | |
| + | X | X | X | X | |
| - | X | X | X | X | |
| * | X | X | |||
| / | X | X | |||
| ( | |||||
| ) | X | X | X | X | X |
Opening and closing parentheses act as operators, although they are not because they do operate on values. But anyway, they can still cause preceding operator to execute. More precisely, closing parenthesis acts similar to an operator with very low precedence. It causes all operators before itself to execute and that process continues until opening parenthesis is reached; at that point the two parentheses cancel each other and they both disappear. Opening parenthesis, conversely, acts as an operator with a very high precedence, causing none of the operators before it to evaluate. It appears like opening parenthesis is an operator which always gets pushed to the stack without triggering any calculation.
And now a word about actual implementation. The notion of preceding operators naturally leads to keeping operators on a stack. In that way we will have access to each operator's predecessor by simply peeking at the top of the stack. Operands would mix with operators any more, but since they must correspond to their assigned operators, we conclude that operands would also need to be pushed to a stack. Operator on top of the operators stack executes on two top-most operands from the operands stack. And once an operator is executed, its resulting value becomes an operand to another operator. This means that evaluated expressions are pushed back onto the operands stack. It is as simple as that. Complete expression evaluation results in an empty operators stack - all operators will be executed - and operands stack containing exactly one value - that is the overall result of evaluating the expression.
Table below simulates this implementation on expression 2*(3+6/2)/4. Note from the figure that we are not on the course of building the expression tree any more. We are now actually evaluating all operations instead of building the tree, because our goal is to write a function which evaluates the expression. Anyway, benefit from expression trees is enormous. Expression evaluation differs from tree building only in piece that decides what to do with operation and its operands. Expression tree builder creates an operation node and adds operands as its child nodes; expression evaluator, on the other hand, evaluates the operation on its operands and produces the resulting value.
| Input character | Action | Operands stack | Operators stack |
|---|---|---|---|
| 2 | Push 2 to operands stack | 2 | (empty) |
| * | Push * to operators stack | 2 | * |
| ( | Push ( to operators stack | 2 | *, ( |
| 3 | Push 3 to operands stack | 2, 3 | *, ( |
| + | Push + to operators stack | 2, 3 | *, (, + |
| 6 | Push 6 to operands stack | 2, 3, 6 | *, (, + |
| / | Push / to operators stack | 2, 3, 6 | *, (, +, / |
| 2 | Push 2 to operands stack | 2, 3, 6, 2 | *, (, +, / |
| ) | Pop last operator (/) and its operands (6, 2) from stacks | 2, 3 | *, (, + |
| Evaluate operation (6/2) and push result to operands stack | 2, 3, 3 | *, (, + | |
| Pop last operator (+) and its operands (3, 3) from stacks | 2 | *, ( | |
| Evaluate operation (3+3) and push result to operands stack | 2, 6 | *, ( | |
| Pop opening parenthesis from operators stack and cancel it with closing parenthesis | 2, 6 | * | |
| / | Pop operator with same precedence (*) and its arguments (2, 6) from stacks | (empty) | (empty) |
| Evaluate expression (2*6) and push result to operands stack | 12 | (empty) | |
| Push / to operations stack | 12 | / | |
| 4 | Push 4 to operands stack | 12, 4 | / |
Note that end result shown in the table above is not the one we expected. Last operator, division, was not evaluated! This is simply because there was no operator coming after that one to cause it to execute. Simply put, it looks like the last operator will always remain unprocessed with this solution. Lucky enough, there is one (albeit, fake) operator that causes all other operators to execute: the closing parenthesis. To utilize its powers, we will have to add it at the end of the expression. But to keep the parentheses balanced, corresponding opening parenthesis must precede the whole expression. With this modification, we are now evaluating expression (2*(3+6/2)/4) instead of the original one. Now even the last operator will be processed, leaving the stacks in the expected state - with empty operators stack and operands stack containing a single value (3 in our example).
And here are the implementation details regarding the added parentheses. Opening parenthesis will be added implicitly - operators stack will initially contain one opening parenthesis. Closing parenthesis will also be added implicitly by iterating one position further than the end of the input string and assuming that the one character off-limits is the closing parenthesis itself. In that way, original expression will remain intact, but it will still act as being enclosed in a pair of parentheses.
One final note remains before we get onto producing the requested function. All examples given this far contained only single-digit numbers. Implementation which follows pays attention to correctly append multiple digits in a single number.
At last, below is the function which evaluates arithmetic expressions. It uses a number of helper functions dedicated to partial tasks that all together lead to calculating final value of the expression. This is the list of all functions that will be implemented:
- EvaluateExpression - This is the main function which receives an expression in form of an array of characters and returns a number which is the final value of the expression.
- ProcessClosingParenthesis - causes all operations on operators stack to execute in reverse order of their appearance; operation stops when opening parenthesis remains on top of the operators stack, after which opening parenthesis is simply popped off the stack to cancel with the closing parenthesis. Main function calls this function whenever it encounters a closing parenthesis.
- ProcessInputNumber - Main function calls this function whenever it encounters a digit. Function extracts one or more consecutive digits from the input number and forms a valid number which is then pushed to the operands stack. Function returns new input position, because it may have advanced by more than one position through the input.
- ProcessInputOperator - Called whenever an operator appears on input. Compares the operator with any operator found on top of the operators stack and, if previous operator should be executed, calls the ExecuteOperation function to collapse the operator on top of the operators stack. This may cause zero, one or more of the previous operators to be executed, depending on relative precedence of the operators. When this process ends, current operator is simply pushed onto the operators stack.
- OperatorCausesExecution - Function receives current operator and an operator appearing on top of the stack and returns true or false value to indicate whether current operator causes previous operator to be executed or not. This function effectively implements the precedence table provided above.
- ExecuteOperation - This function should be called when operator on top of the operators stack should be executed. Function pops two values from the operands stack and one operator from the operators stack. After that, depending on which operator has been popped, executes the appropriate operation and pushes the result back to the operands stack.
Now that we have explained purpose of all functions, we can provide their pseudo-code:
function EvaluateExpression(exp, n)
exp - expression, array of characters with indices 0..n-1
n - number of letters in the expression
begin
vStack - stack of values (operands)
opStack - stack of operators
opStack.push("(") -- implicit open parenthesis
pos = 0 -- current position in input array
while pos <= n
begin
if pos = n OR exp[pos] = ")" then
pos = ProcessClosingParenthesis(vStack, opStack)
pos = pos + 1
else if exp[pos] is a digit then
pos = ProcessInputNumber(exp, n, pos, vStack)
else
ProcessInputOperator(exp[pos], vStack, opStack)
pos = pos + 1
end
return vStack.Pop() -- remaining value is the expression result
end
function ProcessClosingParenthesis(vStack, opStack)
vStack - stack of operands
opStack - stack of operators
begin
while top of opStack is not "("
ExecuteOperation(vStack, opStack)
opStack.Pop() -- Remove the opening parenthesis
end
function ProcessInputNumber(exp, n, pos, vStack)
exp - array of characters representing arithmetic expression
n - length of exp
pos - position of the first digit in the number
vStack - stack of values
begin
value = 0
while pos < n AND exp[pos] is a digit
begin
value = 10 * value + exp[pos]
pos = pos + 1
end
vStack.Push(value)
return pos
end
function ProcessInputOperator(op, vStack, opStack)
op - character representing operator to execute
vStack - stack of operands
opStack - stack of operators
begin
while opStack is not empty AND OperatorCausesEvaluation(op, top of opStack)
ExecuteOperation(vStack, opStack)
opStack.Push(op)
end
function OperatorCausesEvaluation(op, prevOp)
op - operator currently being processed
prevOp - previous operator which might be processed
begin
evaluate = false
if op = "+" AND prevOp <> "(" then
evaluate = true
else if op = "-" AND prevOp <> "(" then
evaluate = true
else if op = "*" AND (prevOp = "*" OR prevOp = "/") then
evaluate = true
else if op = "/" AND (prevOp = "*" OR prevOp = "/") then
evaluate = true
else if op = ")" then
evaluate = true
return evaluate
end
function ExecuteOperation(vStack, opStack)
vStack - stack of operands
opStack - stack of operators
begin
rightOperand = vStack.Pop()
leftOperand = vStack.Pop()
op = opStack.Pop()
if op = "+" then
value = leftOperand + rightOperand
else if op = "-" then
value = leftOperand - rightOperand
else if op = "*" then
value = leftOperand * rightOperand
else if op = "/" then
value = leftOperand / rightOperand
vStack.Push(value)
end
The code is fairly long, mainly due to effort put into breaking the overall operation into simpler steps. This has lead to a reasonably simple main function, but also to a long list of helper functions. Anyway, this solution should perform well on all well-formed arithmetic expressions.
Implementation
Below is the full implementation of EvaluateExpression function and its helpers in C#.
int EvaluateExpression(char[] exp)
{
Stack<int> vStack = new Stack<int>();
Stack<char> opStack = new Stack<char>();
opStack.Push('('); // Implicit opening parenthesis
int pos = 0;
while (pos <= exp.Length)
{
if (pos == exp.Length || exp[pos] == ')')
{
ProcessClosingParenthesis(vStack, opStack);
pos++;
}
else if (exp[pos] >= '0' && exp[pos] <= '9')
{
pos = ProcessInputNumber(exp, pos, vStack);
}
else
{
ProcessInputOperator(exp[pos], vStack, opStack);
pos++;
}
}
return vStack.Pop(); // Result remains on values stacks
}
void ProcessClosingParenthesis(Stack<int> vStack,
Stack<char> opStack)
{
while (opStack.Peek() != '(')
ExecuteOperation(vStack, opStack);
opStack.Pop(); // Remove the opening parenthesis
}
int ProcessInputNumber(char[] exp, int pos,
Stack<int> vStack)
{
int value = 0;
while (pos < exp.Length &&
exp[pos] >= '0' && exp[pos] <= '9')
value = 10 * value + (int)(exp[pos++] - '0');
vStack.Push(value);
return pos;
}
void ProcessInputOperator(char op, Stack<int> vStack,
Stack<char> opStack)
{
while (opStack.Count > 0 &&
OperatorCausesEvaluation(op, opStack.Peek()))
ExecuteOperation(vStack, opStack);
opStack.Push(op);
}
bool OperatorCausesEvaluation(char op, char prevOp)
{
bool evaluate = false;
switch (op)
{
case '+':
case '-':
evaluate = (prevOp != '(');
break;
case '*':
case '':
evaluate = (prevOp == '*' || prevOp == '');
break;
case ')':
evaluate = true;
break;
}
return evaluate;
}
void ExecuteOperation(Stack<int> vStack,
Stack<char> opStack)
{
int rightOperand = vStack.Pop();
int leftOperand = vStack.Pop();
char op = opStack.Pop();
int result = 0;
switch (op)
{
case '+':
result = leftOperand + rightOperand;
break;
case '-':
result = leftOperand - rightOperand;
break;
case '*':
result = leftOperand * rightOperand;
break;
case '':
result = leftOperand rightOperand;
break;
}
vStack.Push(result);
}Observe how implementation of functions OperationCausesEvaluation and ExecuteOperation has shifted to be closer to the spirit of C# coding. But logic has remained the same as it was in the pseudo-code.
Demonstration
We could write a very simple console application which demonstrates work of the EvaluateExpression function. Here is one possible implementation:
using System;
using System.Collections.Generic;
namespace ExpressionEvaluator
{
public class Program
{
static int EvaluateExpression(char[] exp)
{
...
}
static void ProcessClosingParenthesis(Stack<int> vStack,
Stack<char> opStack)
{
...
}
static int ProcessInputNumber(char[] exp, int pos,
Stack<int> vStack)
{
...
}
static void ProcessInputOperator(char op, Stack<int> vStack,
Stack<char> opStack)
{
...
}
static bool OperatorCausesEvaluation(char op, char prevOp)
{
...
}
static void ExecuteOperation(Stack<int> vStack,
Stack<char> opStack)
{
...
}
public static void Main(string[] args)
{
while (true)
{
Console.Write("Enter expression (ENTER to exit): ");
string line = Console.ReadLine();
if (string.IsNullOrEmpty(line))
break;
char[] exp = line.ToCharArray();
int value = EvaluateExpression(exp);
Console.WriteLine("{0}={1}", line, value);
}
}
}
}
When this application is run, it produces the following output:
Enter expression (ENTER to exit): 2
2=2
Enter expression (ENTER to exit): 2+3
2+3=5
Enter expression (ENTER to exit): 2+3*4
2+3*4=14
Enter expression (ENTER to exit): 2*3+4
2*3+4=10
Enter expression (ENTER to exit): 2*6/4
2*6/4=3
Enter expression (ENTER to exit): 2*(3+6/2)/4
2*(3+6/2)/4=3
Enter expression (ENTER to exit):
Follow-Up Exercises
Readers are suggested to build upon this solution and work up solutions to extended tasks:
- Allow blank spaces in input expressions.
- Implement exponentiation represented by operator ^. Keep on mind that this operation is associative from right to left, i.e. a^b^c=a^(b^c).
- Add support for fractional numbers. When division operation is applied to operands that are not divisible without remainder, keep the result as a fractional number. For example, expression 2*(3+6/2)/5 evaluates to 12/5, rather than 2.
If you wish to learn more, please watch my latest video courses

Beginning Object-oriented Programming with C#
In this course, you will learn the basic principles of object-oriented programming, and then learn how to apply those principles to construct an operational and correct code using the C# programming language and .NET.
As the course progresses, you will learn such programming concepts as objects, method resolution, polymorphism, object composition, class inheritance, object substitution, etc., but also the basic principles of object-oriented design and even project management, such as abstraction, dependency injection, open-closed principle, tell don't ask principle, the principles of agile software development and many more.
More...

Design Patterns in C# Made Simple
In this course, you will learn how design patterns can be applied to make code better: flexible, short, readable.
You will learn how to decide when and which pattern to apply by formally analyzing the need to flex around specific axis.
More...

Refactoring to Design Patterns
This course begins with examination of a realistic application, which is poorly factored and doesn't incorporate design patterns. It is nearly impossible to maintain and develop this application further, due to its poor structure and design.
As demonstration after demonstration will unfold, we will refactor this entire application, fitting many design patterns into place almost without effort. By the end of the course, you will know how code refactoring and design patterns can operate together, and help each other create great design.
More...

Mastering Iterative Object-oriented Development in C#
In four and a half hours of this course, you will learn how to control design of classes, design of complex algorithms, and how to recognize and implement data structures.
After completing this course, you will know how to develop a large and complex domain model, which you will be able to maintain and extend further. And, not to forget, the model you develop in this way will be correct and free of bugs.
More...
About

Zoran Horvat is the Principal Consultant at Coding Helmet, speaker and author of 100+ articles, and independent trainer on .NET technology stack. He can often be found speaking at conferences and user groups, promoting object-oriented and functional development style and clean coding practices and techniques that improve longevity of complex business applications.
Elsewhere
Video Courses
- Making Your C# Code More Object-oriented
- Beginning Object-oriented Programming with C#
- Collections and Generics in C#
- Design Patterns in C# Made Simple
- Refactoring to Design Patterns
- Mastering Iterative Object-oriented Programming in C#
- Making Your C# Code More Functional
- Making Your Java Code More Object-oriented
- Writing Purely Functional Code in C#
- Tactical Design Patterns in .NET: Creating Objects
- Tactical Design Patterns in .NET: Control Flow
- Tactical Design Patterns in .NET: Managing Responsibilities
- Advanced Defensive Programming Techniques
- Writing Highly Maintainable Unit Tests
- Improving Testability Through Design
Articles
- Here is Why Calling a Virtual Function from the Constructor is a Bad Idea
- What Makes List<T> So Efficient in .NET?
- Nondestructive Mutation and Records in C#
- Understanding Covariance and Contravariance of Generic Types in C#
- Using Record Types in C#
- Unit Testing Case Study: Calculating Median
- More...