How to Apply Visitor Pattern Without Breaking Encapsulation of Concrete Elements
by Zoran Horvat
Visitor pattern lets you add an operation to a hierarchy of classes in such a way that existing classes need not be modified. In this article we are assuming that readers are well acquainted with the Visitor pattern ( http://en.wikipedia.org/wiki/Visitor_pattern ). Problem with the Visitor pattern as it is presented in the Gang of Four book is that it breaks encapsulation. Namely, objects that are visited must let the visitor read their internal state. And, if visitor can do that, in most programming languages it means that anyone else can do the same as well. Consequently, classes that fulfill the Element role in the Visitor pattern would clearly break guidelines of object-oriented design.
Note that original authors were perfectly aware of this problem. Here is the quote:
Visitor's approach assumes that the ConcreteElement interface is
powerful enough to let visitors do their job. As a result, the pattern
often forces you to provide public operations that access an element's
internal state, which may compromise its encapsulation.
Gamma et al, Design Patterns: Elements of Reusable Object-Oriented Software,
Addison-Wesley 1995, pp. 337
In this article we are going to present one specific implementation of the Visitor pattern. It lets us keep Element type encapsulate its state, while still providing sufficient information to the visitor to perform its operation.
As an example, observe a system which produces some kinds of values - for example a script interpreter. Value can be virtually anything: integer number, decimal number, fraction, complex number; or even something that is not a number at all - string, vector, matrix, polar coordinates. Values are combined using operations, such as addition, multiplication, division, etc.
One view of such a system is to define an interface IValue and then add operations to it:
interface IValue
{
IValue Add(IValue other);
IValue Subtract(IValue other);
IValue Divide(IValue other);
...
}
This approach exhibits several problems. List of possible operations can be quite long, adding burden to the implementation which starts growing indefinitely. But even worse problem is that operations are receiving an abstract IValue and therefore cannot be implemented in even remotely elegant way. For example, Add operation in integer number would have to know about decimal numbers, fractions, complex numbers, and even about strings, vectors and other types. In each case, a completely different type of IValue is returned from the Add method. To make things worse, those types would also have to be aware of the integer number, which produces circular dependencies between them.
One way to deal with the problem is to externalize operations by applying the Visitor pattern to values:
interface IValue
{
string Format();
void Accept(IValueVisitor visitor);
}
In this implementation, value has only a single responsibility and that is to format itself neatly so that it can be presented in the user interface. One might object and request the formatting responsibility to be implemented in a separate Formatter class. That would be a legitimate objection, but let's leave it aside right now and focus on operations among values.
Operations would now be encapsulated in Visitors - one operation per concrete Visitor. Each visitor would have to be aware of all Concrete Elements, such as integer number, fraction, complex number, vector, string, etc. Its responsibility would be to convert values to a common type and then perform the operations. Return value would again be some Concrete Element, which is the simplest concrete value type which can encapsulate the operation result. For example, summation of two fractions 1/2 and 3/2 would produce an integer value 2, rather than a fraction 4/2 or 2/1. That neatly meets user's expectation that fractions will be magically reduced before operation result is produced to the screen. Figure below shows a sequence of arithmetic operations that include fractional numbers, but eventually yield an integer result.
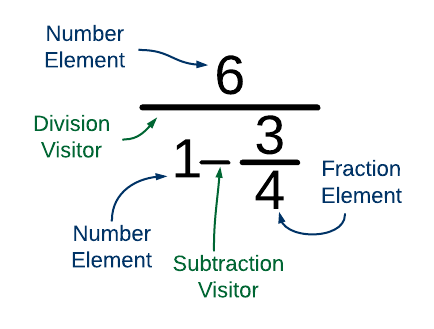
Now comes the critical part. If operations, such as division and subtraction, are implemented in the visitor, how can the visitor access content of each value. Values do not expose their content: Number does not specify its integer value; Fraction does not expose its numerator and denominator. One way out of the troubles is to design the visitor so that it does not receive concrete instances, but rather their encapsulated values:
interface IValueVisitor
{
void VisitNumber(int number);
void VisitFraction(int numerator, int denominator);
}
In this way, concrete elements can remain closed for external access, while visitors can freely perform their operations.
Here is the implementation of concrete value classes and corresponding value factory.
interface IValue
{
string Format();
void Accept(IValueVisitor visitor);
}
interface IValueVisitor
{
void VisitNumber(int number);
void VisitFraction(int numerator, int denominator);
}
interface IValueFactory
{
IValue CreateNumber(int number);
IValue CreateFraction(int numerator, int denominator);
}
class Number : IValue
{
private int value;
public Number(int value)
{
this.value = value;
}
public string Format()
{
return this.value.ToString("0");
}
public void Accept(IValueVisitor visitor)
{
visitor.VisitNumber(this.value);
}
}
class Fraction : IValue
{
private int numerator;
private int denominator;
public Fraction(int numerator, int denominator)
{
this.numerator = numerator;
this.denominator = denominator;
}
public string Format()
{
return string.Format("{0} / {1}", this.numerator, this.denominator);
}
public void Accept(IValueVisitor visitor)
{
visitor.VisitFraction(this.numerator, this.denominator);
}
}
class ValueFactory : IValueFactory
{
public IValue CreateNumber(int number)
{
return new Number(number);
}
public IValue CreateFraction(int numerator, int denominator)
{
return new Fraction(numerator, denominator);
}
}
Both Number and Fraction are immutable implementations of the IValue interface. And both fully encapsulate their state, without letting the external clients see actual numeric values that they represent. The only operation exposed is the Format method, which can be used to print the value to the screen, for example. Of course, there is also the Accept operation, which implements value's role in the Visitor pattern.
And thus we come to the point when concrete visitors should be implemented. In order to execute expression 6 / (1 - 3/4), we need subtraction and division. Both operations must support both existing numeric types: integer numbers and fractional numbers. Here is implementation of the subtraction operation:
class DifferenceValue : IValue, IValueVisitor
{
private int numerator;
private int denominator;
private int lastNumerator;
private int lastDenominator;
private IValue internalValue;
public DifferenceValue(IValueFactory factory, IValue a, IValue b)
{
VisitLeftOperand(a);
VisitRightOperand(b);
ReduceAndCreateValue(factory);
}
private void VisitLeftOperand(IValue a)
{
a.Accept(this);
this.numerator = this.lastNumerator;
this.denominator = this.lastDenominator;
}
private void VisitRightOperand(IValue b)
{
b.Accept(this);
this.numerator =
this.numerator * this.lastDenominator -
this.lastNumerator * this.denominator;
this.denominator *= this.lastDenominator;
}
private void ReduceAndCreateValue(IValueFactory factory)
{
ReduceFraction();
CreateValue(factory);
}
private void ReduceFraction()
{
int gcd = MathUtils.GreatestCommonDivisor(this.numerator,
this.denominator);
this.numerator /= gcd;
this.denominator /= gcd;
}
private void CreateValue(IValueFactory factory)
{
if (this.denominator == 1)
this.internalValue = factory.CreateNumber(this.numerator);
else
this.internalValue = factory.CreateFraction(this.numerator,
this.denominator);
}
public string Format()
{
return this.internalValue.Format();
}
public void Accept(IValueVisitor visitor)
{
this.internalValue.Accept(visitor);
}
public void VisitNumber(int number)
{
this.lastNumerator = number;
this.lastDenominator = 1;
}
public void VisitFraction(int numerator, int denominator)
{
this.lastNumerator = numerator;
this.lastDenominator = denominator;
}
}
This implementation relies on a utility class which can calculate greatest common divisor:
static class MathUtils
{
public static int GreatestCommonDivisor(int a, int b)
{
if (a < b)
return GreatestCommonDivisor(b, a);
while (b > 0)
{
int tmp = a % b;
a = b;
b = tmp;
}
return a;
}
}
There are a couple of important concepts wrapped in this class. First, it implements both the IValue and IValueVisitor interfaces. Consequently, instances of this class can be used as yet another abstract value, which means that result of a subtraction can be incorporated in larger expressions. Second, it implements IValueVisitor so that it can access internal state of both of its operands. That is how the subtraction operation is implemented internally. Since we only support integer and fractional numbers, subtraction operation assumes integer number N as a fraction N/1 and then performs fractional subtraction. However, just after the operation is done, it attempts to reduce the fraction and, if it becomes something like M/1, to convert it back to an integer number. If denominator is greater than one, however, the overall subtraction result will remain a fraction. This is how we have provided a guarantee that result of the operation is of the simplest possible type for a given arithmetic value. In other words, two Fraction operands, such as 3/2 and 1/2, can be subtracted to produce an Integer object encapsulating value 1, rather than a Fraction instance as input operands are.
Likewise, we can implement the division operation:
class DivisionValue: IValue, IValueVisitor
{
private IValue internalValue;
private int numerator;
private int denominator;
private int lastNumerator;
private int lastDenominator;
public DivisionValue(IValueFactory factory, IValue a, IValue b)
{
VisitLeftOperand(a);
VisitRightOperand(b);
ReduceAndCreateValue(factory);
}
private void VisitLeftOperand(IValue operand)
{
operand.Accept(this);
this.numerator = this.lastNumerator;
this.denominator = this.lastDenominator;
}
private void VisitRightOperand(IValue operand)
{
operand.Accept(this);
this.numerator *= this.lastDenominator;
this.denominator *= this.lastNumerator;
}
private void ReduceAndCreateValue(IValueFactory factory)
{
int gcd = MathUtils.GreatestCommonDivisor(this.numerator,
this.denominator);
this.numerator /= gcd;
this.denominator /= gcd;
CreateValue(factory);
}
private void CreateValue(IValueFactory factory)
{
if (this.denominator == 1)
this.internalValue = factory.CreateNumber(this.numerator);
else
this.internalValue = factory.CreateFraction(this.numerator,
this.denominator);
}
public void VisitNumber(int number)
{
this.lastNumerator = number;
this.lastDenominator = 1;
}
public void VisitFraction(int numerator, int denominator)
{
this.lastNumerator = numerator;
this.lastDenominator = denominator;
}
public string Format()
{
return this.internalValue.Format();
}
public void Accept(IValueVisitor visitor)
{
this.internalValue.Accept(visitor);
}
}
If needed, we could produce any other operation by only producing new concrete Visitors:
- Addition - f(a, b) = a + b
- Multiplication - f(a, b) = a * b
- Reciprocal - f(x) = 1/x
- Negation - f(x) = -x
Possibilities are almost endless. They are rather limited by the domain from which we are pulling the values, which is the set of rational numbers. This means that we cannot implement logarithm function or power function, or at least not before we introduce real numbers as another concrete element. Good side of this design is that none of the concrete element classes, nor the IValue interface need be modified when new operation is added.
Finally, just as a matter of convenience, we could define abstract factory for operation visitors:
interface IAggregateValueFactory
{
IValue Subtract(IValue a, IValue b);
IValue Divide(IValue a, IValue b);
}
class AggregateValueFactory : IAggregateValueFactory
{
private IValueFactory factory;
public AggregateValueFactory(IValueFactory factory)
{
this.factory = factory;
}
public IValue Subtract(IValue a, IValue b)
{
return new DifferenceValue(this.factory, a, b);
}
public IValue Divide(IValue a, IValue b)
{
return new DivisionValue(this.factory, a, b);
}
}
This factory lets us use subtraction and division like operations, which completely hides the fact that DifferenceValue and DivisionValue are concrete visitors. That can also be viewed as an application of the Interface Segregation Principle (ISP), because concrete visitors have twofold purpose which is inherited from two distinct interfaces.
Now let's demonstrate use of these classes:
class Program
{
static void Main()
{
IValueFactory plain = new ValueFactory();
IAggregateValueFactory aggregate =
new AggregateValueFactory(plain);
IValue result =
aggregate.Divide(
plain.CreateNumber(6),
aggregate.Subtract(
plain.CreateNumber(1),
aggregate.Divide(
plain.CreateNumber(3),
plain.CreateNumber(4)
)
)
); // expression: 6 / (1 - 3/4)
Console.WriteLine("6 / (1 - 3/4) = {0}", result.Format());
// Integer 24, not fraction 24/1
Console.ReadLine();
}
}
6 / (1 - 3/4) = 24
The overall result is obviously an instance of the Number class, although the process that produces the result involves two operations on fractions. Clients that access IValue instances are completely unaware of type conversions that take place behind the scenes. This is because calculations and type selections are well protected by encapsulation. If you wish to learn more, please watch my latest video courses

Beginning Object-oriented Programming with C#
In this course, you will learn the basic principles of object-oriented programming, and then learn how to apply those principles to construct an operational and correct code using the C# programming language and .NET.
As the course progresses, you will learn such programming concepts as objects, method resolution, polymorphism, object composition, class inheritance, object substitution, etc., but also the basic principles of object-oriented design and even project management, such as abstraction, dependency injection, open-closed principle, tell don't ask principle, the principles of agile software development and many more.
More...

Design Patterns in C# Made Simple
In this course, you will learn how design patterns can be applied to make code better: flexible, short, readable.
You will learn how to decide when and which pattern to apply by formally analyzing the need to flex around specific axis.
More...

Refactoring to Design Patterns
This course begins with examination of a realistic application, which is poorly factored and doesn't incorporate design patterns. It is nearly impossible to maintain and develop this application further, due to its poor structure and design.
As demonstration after demonstration will unfold, we will refactor this entire application, fitting many design patterns into place almost without effort. By the end of the course, you will know how code refactoring and design patterns can operate together, and help each other create great design.
More...

Mastering Iterative Object-oriented Development in C#
In four and a half hours of this course, you will learn how to control design of classes, design of complex algorithms, and how to recognize and implement data structures.
After completing this course, you will know how to develop a large and complex domain model, which you will be able to maintain and extend further. And, not to forget, the model you develop in this way will be correct and free of bugs.
More...
About

Zoran Horvat is the Principal Consultant at Coding Helmet, speaker and author of 100+ articles, and independent trainer on .NET technology stack. He can often be found speaking at conferences and user groups, promoting object-oriented and functional development style and clean coding practices and techniques that improve longevity of complex business applications.
Elsewhere
Video Courses
- Making Your C# Code More Object-oriented
- Beginning Object-oriented Programming with C#
- Collections and Generics in C#
- Design Patterns in C# Made Simple
- Refactoring to Design Patterns
- Mastering Iterative Object-oriented Programming in C#
- Making Your C# Code More Functional
- Making Your Java Code More Object-oriented
- Writing Purely Functional Code in C#
- Tactical Design Patterns in .NET: Creating Objects
- Tactical Design Patterns in .NET: Control Flow
- Tactical Design Patterns in .NET: Managing Responsibilities
- Advanced Defensive Programming Techniques
- Writing Highly Maintainable Unit Tests
- Improving Testability Through Design
Articles
- Here is Why Calling a Virtual Function from the Constructor is a Bad Idea
- What Makes List<T> So Efficient in .NET?
- Nondestructive Mutation and Records in C#
- Understanding Covariance and Contravariance of Generic Types in C#
- Using Record Types in C#
- Unit Testing Case Study: Calculating Median
- More...