Sudoku Solver
by Zoran Horvat
Problem Statement
Goal of this exercise is to write code which solves 9x9 Sudoku board. Program receives initial Sudoku as a sequence of nine lines of text. On output, program produces solved Sudoku.
Example: Suppose that the following sequence of lines is provided on input:
...7..3.1
3..9.....
.4.31.2..
.6.4..5..
.........
..1..8.4.
..6.21.5.
.....9..8
8.5..4...
Program should solve this puzzle and produce output:
589742361
312986475
647315289
268493517
493157826
751268943
936821754
124579638
875634192
Keywords: Sudoku, search, depth-first search, constraint satisfaction, most constrained first heuristic.
Problem Analysis
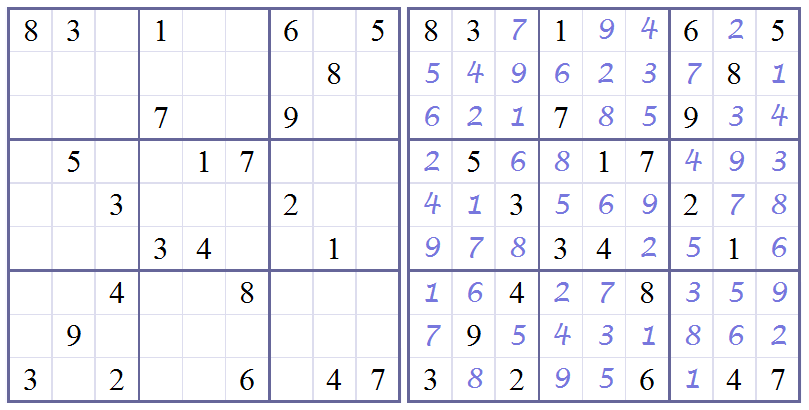
Sudoku table consists of 9x9 cells, each cell receiving a single digit between 1 and 9, inclusive. Sub-tables consisting of 3x3 cells are specifically grouped, as shown on the picture below. In order to be solved correctly, Sudoku table must satisfy seemingly simple criteria: on every row, every column and every 3x3 block, each digit must appear exactly once. Picture shows starting position and corresponding Sudoku table when solved (source: http://www.websudoku.com ).
The problem here is how to solve a given Sudoku so that final state of the table satisfies the validation criteria. One possible solution is to search through partial solutions in depth-first manner. In each step we pick up one empty cell in the table and try to put any digit that wouldn't cause a constraint violation. If successful, we simply repeat the operation recursively, on a table which has one empty cell less than before. Should this process come to a dead-end, in which there is such a cell in which no digit can be placed lest to cause a violation, we unroll the process back one step and try to replace the last digit with the next viable candidate, if such digit exists; otherwise, we unroll one step more to try next candidate one level further up the line. In perspective, we hope to search all possibilities until final solution to the Sudoku is found. On the bitter end, we might finish the search without encountering the fully populated table, in which case we simply conclude that initial position was not valid.
But now there appears to be a problem. Sudoku table contains 81 cells, most of which are initially blank (57 in the example shown in the picture above). How many tables should we consider before the solution is found? With every step deeper down the search tree, number of tables considered becomes larger and larger - actually it grows exponentially with depth of the search tree. Going down fifty or so steps into depth sounds quite unfeasible. So what should we do to reduce number of tables generated by the algorithm?
There is one simple solution which is applicable to many search problems. At every step we should choose the cell in the table which offers smallest number of candidates, i.e. digits that do not generate collision immediately. By looking for such heavily constrained cells we hope to provoke collisions early in the search, while tree is still shallow and number of nodes reasonably small. This search strategy is called "most constrained first" heuristic, deriving its name from the occasion that cell with most constraints upon itself is chosen first in each step of the algorithm. When properly applied, this heuristic can cause such tremendous drop in number of search steps that once unfeasible search scheme becomes fast enough to be used in practice.
Algorithm which solves the Sudoku table is now quite simple. It boils down to a function which solves a single cell and then calls itself recursively, trying another candidate each time when recursive call returns failure condition. Here is the pseudo-code:
function Solve(table)
begin
c = cell with smallest number of candidates
if c not found then
return success (there are no empty cells - puzzle is solved)
for each d in candidates(c)
begin
set value of cell c to d
status = Solve(table)
if status = success then
return success
else
Clear cell c
end
return failure (no solution was found or c had empty candidates set)
end
Implementation
Solver algorithm has proven to be very short. But is it efficient enough to actually produce a valid solution to a realistic Sudoku table? We will soon find that out from the implementation that follows. Note that actual implementation contains functions that load and print the Sudoku table, but it also contains implementation of a function that extracts list of candidates for a given table cell. This utility function was skipped in pseudo-code provided in previous section, but now we had to implement it in order to make the solution complete.
using System;
namespace Sudoku
{
class Program
{
static char[][] LoadTable()
{
char[][] table = new char[9][];
Console.WriteLine("Enter Sudoku table:");
for (int i = 0; i < 9; i++)
{
string line = Console.ReadLine();
table[i] = line.PadRight(9).Substring(0, 9).ToCharArray();
for (int j = 0; j < 9; j++)
if (table[i][j] < '0' || table[i][j] > '9')
table[i][j] = '.';
}
return table;
}
static void PrintTable(char[][] table, int stepsCount)
{
Console.WriteLine();
Console.WriteLine("Solved table after {0} steps:", stepsCount);
for (int i = 0; i < 9; i++)
Console.WriteLine("{0}", new string(table[i]));
}
static char[] GetCandidates(char[][] table, int row, int col)
{
string s = "";
for (char c = '1'; c <= '9'; c++)
{
bool collision = false;
for (int i = 0; i < 9; i++)
{
if (table[row][i] == c ||
table[i][col] == c ||
table[(row - row % 3) + i / 3][(col - col % 3) + i % 3] == c)
{
collision = true;
break;
}
}
if (!collision)
s += c;
}
return s.ToCharArray();
}
static bool Solve(char[][] table, ref int stepsCount)
{
bool solved = false;
int row = -1;
int col = -1;
char[] candidates = null;
for (int i = 0; i < 9; i++)
for (int j = 0; j < 9; j++)
if (table[i][j] == '.')
{
char[] newCandidates = GetCandidates(table, i, j);
if (row < 0 || newCandidates.Length < candidates.Length)
{
row = i;
col = j;
candidates = newCandidates;
}
}
if (row < 0)
{
solved = true;
}
else
{
for (int i = 0; i < candidates.Length; i++)
{
table[row][col] = candidates[i];
stepsCount++;
if (Solve(table, ref stepsCount))
{
solved = true;
break;
}
table[row][col] = '.';
}
}
return solved;
}
static void Main(string[] args)
{
while (true)
{
char[][] table = LoadTable();
int stepsCount = 0;
if (Solve(table, ref stepsCount))
PrintTable(table, stepsCount);
else
Console.WriteLine("Could not solve this Sudoku.");
Console.WriteLine();
Console.Write("More? (y/n) ");
if (Console.ReadLine().ToLower() != "y")
break;
}
}
}
}
Demonstration
When source code provided above is compiled and run, it lets the user enter initial Sudoku position and then prints the solved table, if solution was found. In addition, total number of different tables produced during the search is printed, in order to prove efficiency of the most constrained first search heuristic.
Enter Sudoku table:
...7..3.1
3..9.....
.4.31.2..
.6.4..5..
.........
..1..8.4.
..6.21.5.
.....9..8
8.5..4...
Solved table after 149 steps:
589742361
312986475
647315289
268493517
493157826
751268943
936821754
124579638
875634192
More? (y/n) y
Enter Sudoku table:
..19...46
3.27..51.
.....4.3.
528.71...
..3.4.6..
...39.725
.5.2.....
.67..94.3
83...51..
Solved table after 46 steps:
781953246
342786519
695124837
528671394
973542681
416398725
154237968
267819453
839465172
More? (y/n) y
Enter Sudoku table:
83.1..6.5
.......8.
...7..9..
.5..17...
..3...2..
...34..1.
..4..8...
.9.......
3.2..6.47
Solved table after 80 steps:
837194625
549623781
621785934
256817493
413569278
978342516
164278359
795431862
382956147
More? (y/n) n
Observe how small is the number of steps required to solve each of these three examples: 149, 46 and 80. This looks almost within the reach of pen-and-paper solver, and it's all thanks to a very efficient search heuristic.
Follow-Up Exercises
Readers are suggested to build upon this solution and work up solutions to extended tasks:
- Modify the solver to try to find more than one solution to a given Sudoku. Success to find multiple solutions indicates that initial table was not valid - correctly formed Sudoku problem should have only one valid solution. Pay close attention to cut-off criterion, i.e. condition under which solution claims that there are multiple solutions. Do not let the solution hang till the end of the Universe when faced with a completely empty table.
- Modify the solver so that it can generate a completely solved Sudoku table starting from an empty table. Make sure that solution does not produce the same solution every time when run!
- Write code which starts from a completely solved puzzle and works its way backwards randomly picking redundant digits and removing it from the table until no more digits can be removed without producing a table with multiple solutions.
If you wish to learn more, please watch my latest video courses

Beginning Object-oriented Programming with C#
In this course, you will learn the basic principles of object-oriented programming, and then learn how to apply those principles to construct an operational and correct code using the C# programming language and .NET.
As the course progresses, you will learn such programming concepts as objects, method resolution, polymorphism, object composition, class inheritance, object substitution, etc., but also the basic principles of object-oriented design and even project management, such as abstraction, dependency injection, open-closed principle, tell don't ask principle, the principles of agile software development and many more.
More...

Design Patterns in C# Made Simple
In this course, you will learn how design patterns can be applied to make code better: flexible, short, readable.
You will learn how to decide when and which pattern to apply by formally analyzing the need to flex around specific axis.
More...

Refactoring to Design Patterns
This course begins with examination of a realistic application, which is poorly factored and doesn't incorporate design patterns. It is nearly impossible to maintain and develop this application further, due to its poor structure and design.
As demonstration after demonstration will unfold, we will refactor this entire application, fitting many design patterns into place almost without effort. By the end of the course, you will know how code refactoring and design patterns can operate together, and help each other create great design.
More...

Mastering Iterative Object-oriented Development in C#
In four and a half hours of this course, you will learn how to control design of classes, design of complex algorithms, and how to recognize and implement data structures.
After completing this course, you will know how to develop a large and complex domain model, which you will be able to maintain and extend further. And, not to forget, the model you develop in this way will be correct and free of bugs.
More...
About

Zoran Horvat is the Principal Consultant at Coding Helmet, speaker and author of 100+ articles, and independent trainer on .NET technology stack. He can often be found speaking at conferences and user groups, promoting object-oriented and functional development style and clean coding practices and techniques that improve longevity of complex business applications.
Elsewhere
Video Courses
- Making Your C# Code More Object-oriented
- Beginning Object-oriented Programming with C#
- Collections and Generics in C#
- Design Patterns in C# Made Simple
- Refactoring to Design Patterns
- Mastering Iterative Object-oriented Programming in C#
- Making Your C# Code More Functional
- Making Your Java Code More Object-oriented
- Writing Purely Functional Code in C#
- Tactical Design Patterns in .NET: Creating Objects
- Tactical Design Patterns in .NET: Control Flow
- Tactical Design Patterns in .NET: Managing Responsibilities
- Advanced Defensive Programming Techniques
- Writing Highly Maintainable Unit Tests
- Improving Testability Through Design
Articles
- Here is Why Calling a Virtual Function from the Constructor is a Bad Idea
- What Makes List<T> So Efficient in .NET?
- Nondestructive Mutation and Records in C#
- Understanding Covariance and Contravariance of Generic Types in C#
- Using Record Types in C#
- Unit Testing Case Study: Calculating Median
- More...